Сценарии поиска решений в данных
Сценарий поиска решения в данных представляет собой процедуру нахождения таких
значений входных параметров, которые приводят к желаемому изменению значения выходного
параметра. При этом одна часть входных параметров фиксируется (факторы, на которые
мы не можем повлиять), а поиск решения осуществляется изменением значений в другой
части входных параметров (факторы, на которые мы можем повлиять). Этот сценарий
используется, например, для планирования действий с целью достижения определенного
значения некоего показателя при заданных ограничениях или для выявления наиболее значимых
факторов, оказывающих влияние на целевую характеристику. В качестве примеров выполнения
таких сценария в бизнес-приложениях могут служить попытки ответить на следующие вопросы:
- какие характеристики клиента в наибольшей степени оказывали влияние на его положительный
отклик на рекламное предложение?
- на какую возрастную группу живущих с родителями молодых людей из
московской области следует ориентироваться в рекламе, чтобы повысить продажи?
Если связь между значениями изменяемых входных параметров и целевой характеристики
известна, т.е. эта связь описывается некой математической функцией, то описанная
задача сводится к нахождению локальной обратной функции. Эта задача решается, обычно,
численными методами и интегрирована во многие программные пакеты, как например,
надстройка Solver в Microsoft Excel. Если же зависимость априорно неизвестна или
же носит стохастический характер, то для ее выявления и инвертирования применяются
различные подходы из области так называемого интеллектуального анализа данных -
Data Mining. Диапазон таких подходов включает как хорошо изученные
статистические методы, так и довольно экзотические пока для большинства
аналитиков методы эволюционного программирования.
В этой статье мы опишем выполнение сценария поиска решений при помощи Байесовских
сетей, а также рассмотрим небольшой пример практического использования
этого подхода с использованием платформы Microsoft Analysis Services 2008.
Байесовская сеть - это направленный ациклический граф, узлами в котором служат
атрибуты. Наличие дуги между атрибутами указывает на наличие между ними непосредственной
(безусловной от других атрибутов) стохастической зависимости. Таким образом, Байесовская
сеть представляет собой модель стохастической зависимости (или, наоборот, условной
стохастической независимости) между атрибутами. Эта модель служит для оценки
совместного распределения данных. Допущения о частичной условной независимости
атрибутов упрощает оценку их совместного распределения и делает эту оценку
более состоятельной при меньшем количестве данных.
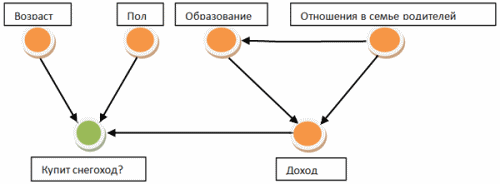
Рис. 1 - Байесовская сеть, описывающая взаимную зависимость атрибутов.
Крайне простой формой обладает так называемая "наивная" Байесовская сеть, для
которой все входные атрибуты условно независимы при условии фиксированного целевого
атрибута. Эта сеть очень легко рассчитывается, но не всегда адекватно описывает совместное распределение.
Существуют также другие специальные формы Байесовских сетей, например, древовидная сеть.
В этом случае, у каждого входного атрибута не могут быть больше одного родителя
из числа других входных атрибутов, при этом зависимость от выходной характеристики может
быть. Структура такой сети определяется максимизацией правдоподобия данных на ее структуре.
В общем случае структуру Байесовской сети можно получить посредством последовательно
выполняемых статистических тестов на условную независимость между тройками всех
атрибутов. Такие тесты позволяют получить так называемое "Марковское одеяло" (Markov blanket)
для каждого узла, т.е. его родителей, детей и других родителей его детей. Этого достаточно,
чтобы реконструировать структуру такой сети.
После того, как структура байесовской сети определена, мы можем получить
оценки совместного распределения вероятностей всех наборов атрибутов. Зная эти
оценки, следующим шагом для выполнения сценария поиска решения мы должны определить
такие значения входного изменяемого набора атрибутов, которые бы максимизировали условную
вероятность того, что целевой атрибут примет выгодное для нас значение. Т.е., если X -
входной набор изменяемых атрибутов, Z = z - входной набор фиксированных атрибутов
со значением z, а Y - целевой атрибут с желательным для нас значением
Y = a, то наша задача заключается в нахождении такого x, при котором
условная вероятность
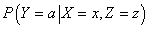 была бы максимальной. Другими словами, мы должны найти
максимум функции была бы максимальной. Другими словами, мы должны найти
максимум функции 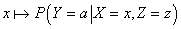 на всей области значений атрибута X. Если это множество значений дискретно
и невелико, то максимум можно найти перебором. В противном случае, следует воспользоваться одним из
итеративных численных алгоритмов нелинейной оптимизации. на всей области значений атрибута X. Если это множество значений дискретно
и невелико, то максимум можно найти перебором. В противном случае, следует воспользоваться одним из
итеративных численных алгоритмов нелинейной оптимизации.
Проиллюстрируем решение этой задаче на демонстрационной базе данных Adventure Works
на платформе Microsoft Analysis Services 2008.
У нас есть таблица со следующей информацией о клиентах:
- семейное положение
- годовой доход
- число детей
- образование
- род занятий
- владелец дома
- число машин
- расстояние до работы
- возраст
- флаг покупки велосипеда - целевой атрибут
-
Создадим структуру данных модели клиентов.
CREATE MINING STRUCTURE [Goal Seek Scenario Structure]
(
[CustomerKey] LONG KEY,
[Семейное положение] TEXT DISCRETE,
[Пол] TEXT DISCRETE,
[Годовой доход] LONG DISCRETIZED,
[Число детей] LONG DISCRETE,
[Образование] TEXT DISCRETE,
[Род занятий] TEXT DISCRETE,
[Владелец дома] TEXT DISCRETE,
[Число машин] LONG DISCRETE,
[Расстояние до работы] TEXT DISCRETE,
[Регион] TEXT DISCRETE,
[Возраст] LONG DISCRETIZED,
[Купит велосипед] LONG DISCRETE
)
-
Создадим модель. К сожалению, из всех байесовских сетей платформой пока поддерживается только "наивный" Байес.
ALTER MINING STRUCTURE [Goal Seek Scenario Structure]
ADD MINING MODEL [Goal Seek Scenario Model]
(
[CustomerKey],
[Семейное положение] PREDICT,
[Пол] PREDICT,
[Годовой доход] PREDICT,
[Число детей] PREDICT,
[Образование] PREDICT,
[Род занятий] PREDICT,
[Владелец дома] PREDICT,
[Число машин] PREDICT,
[Расстояние до работы] PREDICT,
[Регион] PREDICT,
[Возраст] PREDICT,
[Купит велосипед] PREDICT
)
USING Microsoft_Naive_Bayes
-
Обучим модель на имеющихся данных из SQL сервера
INSERT INTO MINING STRUCTURE [Goal Seek Scenario Structure]
(
[CustomerKey],
[Семейное положение],
[Пол],
[Годовой доход],
[Число детей],
[Образование],
[Род занятий],
[Владелец дома],
[Число машин],
[Расстояние до работы],
[Регион],
[Возраст],
[Купит велосипед]
)
OPENROWSET
(
'SQLOLEDB',
'Server=.;Database=AdventureWorksDW;Trusted_Connection=yes;',
'
SELECT
[CustomerKey],
[Семейное положение],
[Пол],
[Годовой доход],
[Число детей],
[Образование],
[Род занятий],
[Владелец дома],
[Число машин],
[Расстояние до работы],
[Регион],
[Возраст],
[Откликнулся на предложение о покупке] AS [Купит велосипед]
FROM
dbo.view_TargetMail
'
)
-
Для выполнения сценария поиска решений среди клиентов, не купивших велосипед, наугад был выбран один.
| CustomerKey | 11198 |
| Семейное положение | Холост |
| Пол | Женский |
| Годовой доход | 70000 |
| Число детей | 4 |
| Образование | Бакалавр |
| Род занятий | Менеджмент |
| Владелец дома | Да |
| Число машин | 1 |
| Расстояние до работы | 10+ Miles |
| Регион | Северная Америка |
| Возраст | 62 |
| Купит велосипед | Нет |
-
Выполним сценарий поиска решения: определить какое расстояние до работы приведет с наибольшей уверенностью к покупке велосипеда при прочих равных характеристиках клиента. Для этого составим запрос, который возвращает условные вероятности покупки велосипеда клиентом с теми же характеристиками, но с различными значениями расстояния до работы и отсортируем результаты по вероятности покупки.
SELECT
t.[Расстояние до работы],
PredictProbability([Купит велосипед], 1) AS [Вероятность покупки]
FROM
[Goal Seek Scenario Model]
NATURAL PREDICTION JOIN
OPENROWSET
(
'SQLOLEDB',
'Server=.;Database=AdventureWorksDW;Trusted_Connection=yes;',
'
SELECT
t1.[Семейное положение],
t1.[Пол],
t1.[Годовой доход],
t1.[Число детей],
t1.[Образование],
t1.[Род занятий],
t1.[Владелец дома],
t1.[Число машин],
t2.[Расстояние до работы],
t1.[Регион],
t1.[Возраст],
t1.[Откликнулся на предложение о покупке] AS [Купит велосипед]
FROM
(
SELECT *
FROM dbo.view_TargetMail
WHERE [CustomerKey] = 11198
) AS t1
CROSS JOIN
(
SELECT DISTINCT [Расстояние до работы]
FROM dbo.view_TargetMail
) AS t2
'
) AS T
ORDER BY PredictProbability([Купит велосипед], 1) DESC
Результат выполнения этого запроса приведен ниже:
| Расстояние до работы | Вероятность покупки |
| 2-5 Miles | 0,51901479376838955 |
| 0-1 Miles | 0,510939808729087 |
| 1-2 Miles | 0,42361558445827235 |
| 5-10 Miles | 0,36267733577732825 |
| 10+ Miles | 0,31911837705263685 |
Таким образом, клиент с теми же прочими характеристиками осуществит покупку велосипеда
с наибольшей вероятностью, если его расстояние до работы будет составлять 2-5 мили.
|


