Системы выработки рекомендаций
Рекомендательные системы (РС) применяются в основном для предложения клиенту в реальном времени продуктов
(фильмов, книг, одежду), которые вероятно его заинтересуют. Особенно широко РС используются в электронной
коммерции. Применение РС-систем расширяется в последнее время на стационарную розничную торговлю, справочные
центры, поиск по программному обеспечению, научным статьям и т.п. Эти применения характеризуются автоматическим
предоставлением рекомендаций пользователям на основании уже совершенных действий (покупок, выставленных рейтингов,
посещений и т.д.) и приемом от них обратной связи (заказы в магазинах, переход по ссылкам и т.п.). Рекомендательные
системы являются одним из важных разделов интеллектуального анализа данных – Data Mining.
Примеры
-
Amazon.com. Если amazon.com не может идентифицировать или еще «не знает» пользователя, то этот
пользователь получит наиболее общие рекомендации. В процессе совершения покупок информация о пользователе
накапливается, что улучшает качество рекомендаций с учетом индивидуальных характеристик клиента. Используется
алгоритм совместной фильтрации, основанной на товарах, матрица показателей сходства товаров (косинусы
углов между векторами товаров (14)) формируется в отложенном режиме.
- Google PageRank. «Похожие» страницы связаны друг с другом, возможно, опосредованной
системой ссылок. Первоначальный алгоритм PageRank не принимал во внимание предпочтения
пользователей, но его расширения и альтернативы могут использовать историю поисковых
запросов и пользовательскую навигацию для улучшения рекомендаций.
Другие примеры: Музыка на Yahoo!, Cinemax.com, Moviecritic, TV Recommender, Video
Guide, CDnow.com и проч.
Сбор данных
В рекомендательных системах используется явный или неявный сбор данных. При явном
сборе от пользователя требуется заполнять опросные анкеты для выявления предпочтений,
а при неявном сборе для выявления предпочтений пользователя и составления рейтингов
происходит автоматическое протоколирование его действий. Самый очевидный способ
неявного сбора информации характерен для систем электронной коммерции, где рейтинг
товара у пользователя оценивается в зависимости от количества заказанных единиц,
включенных пользователем в свой заказ.
Формирование рекомендаций
Различают следующие подходы к формирование рекомендаций:
- На основании содержания – рекомендации формируются для товаров, похожих на товары
уже заказанные клиентом или на товары, заказываемые похожими клиентами. Степень
похожести оценивается на основании характеристик товаров и клиентов. Для товаров
это могут быть сюжет, режиссер, школа (для фильмов); общее музыкальное направление,
стиль (для музыки); функциональное назначение, категория, ценовая группа (для товаров).
Для клиентов характеристики, определяющие их похожесть могут быть демографические
данные, предпочтения из заполненных анкет и т.д. В этом подходе используются методы
кластеризации товаров или клиентов, формирование между ними связей и связанных структур,
а также классификационные алгоритмы Data Mining.
- На основе транзакций – рекомендации формируются на основании пользовательского поведения,
т.е. товары считаются похожими если часто входят совместно в одну транзакцию, а
клиенты считаются похожими если совершают схожие покупки. Системы выработки рекомендаций
на основании транзакций называют системами совместной фильтрации (CF – collaborative
filtering).
Иногда также используется комбинированный подход ([4], [6]). Например, неизвестные
рейтинги исследуемого пользователя вычисляются методом на основании транзакций,
при этом все непроставленные другими пользователями рейтинги учитываются в алгоритме
с применением модели на основании содержания.
Большинство научных публикаций, связанных с алгоритмами рекомендательных систем,
основаны на совместной фильтрации.
Также при формировании рекомендаций используются два следующих подхода:
- Основанный на всех данных (Memory-based) – рекомендации формируются на основании
вычисления некоторой меры по всем накопленным данным. Этот подход проще, показал
высокую точность на практике и обладает преимуществом инкрементального учета новых
данных (новые транзакции просто добавляются в базу данных и учитываются при формировании
прогноза наряду с имеющимися). Однако, этот подход вычислительно сложен с точки
зрения времени и ресурсов памяти. Также, этот подход не может предоставить описательный
анализ существующих закономерностей, дать большее понимание имеющихся данных и объяснить
прогноз.
- Основанный на моделях (Model-based) – сначала формируется описательная модель предпочтений
пользователей, товаров и взаимосвязи между ними, а затем рекомендации формируются
на основании полученной модели. Преимуществом такого подхода является наличие модели,
дающей большее понимание формируемых рекомендаций и наличия взаимосвязей в данных,
а также тот факт, что процесс формирования рекомендаций разбит на два этапа: ресурсоемкое
обучение модели в отложенном режиме и достаточно простое вычисление рекомендаций
на основе существующей модели в реальном времени. Однако, такие модели не поддерживают
инкрементального обучения (появление новых данных требует пересчета всей модели)
и в основном показывают меньшую точность прогноза, чем Memory-based.
Совместная фильтрация
Идея совместной фильтрации (CF) состоит в предположении, что похожие клиенты совершают
схожие покупки, а похожие товары покупаются клиентами совместно.
В этой связи различают два подхода к совместной фильтрации:
- Фильтрация по пользователям (User-centric). В этом случае неизвестный рейтинг товару
выставляется на основании рейтингов, которые были проставлены тому же товару пользователями,
похожими на данного. Этот подход реализуется двумя шагами:
- Найти пользователей, которые совершили аналогичные покупки, как и данный пользователь.
- Предложить товары с максимальным рейтингом среди товаров, выбираемых похожими пользователями.
- Фильтрация по товарам (Item-centric). Неизвестный рейтинг товару выставляется на
основании рейтингов других похожих товаров, уже включенных пользователем в заказ.
Этот подход реализуется двумя шагами:
- Построить матрицу товаров для определения степени схожести между товарами.
- Используя степень схожести предложить товары, похожие на уже заказанные данным пользователем.
- Используется гибридный подход.
Далее мы будем использовать следующие обозначения.
Пусть у нас имеются данные об m товарах и n транзакциях. Обозначим
каждую i-ую транзакцию m-мерным вектором
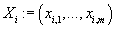 ,
где ,
где
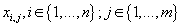 - рейтинг j-того товара, приобретенного в i-ой транзакции, а каждый
j-ый товар n-мерным вектором
- рейтинг j-того товара, приобретенного в i-ой транзакции, а каждый
j-ый товар n-мерным вектором
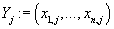 рейтингов j-ого товара во всех транзакциях.
рейтингов j-ого товара во всех транзакциях.
Фильтрация по транзакциям
Если мы рассматриваем набор транзакций
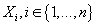 как множество одинаково распределенных независимых случайных величин, то лучшим
(с точки зрения минимизации среднеквадратичной ошибки) прогнозом заказа j-ого
товара на u-ой транзакции, u>n в виде константы будет значение математического
ожидания соответствующий случайной величины, т.е.
как множество одинаково распределенных независимых случайных величин, то лучшим
(с точки зрения минимизации среднеквадратичной ошибки) прогнозом заказа j-ого
товара на u-ой транзакции, u>n в виде константы будет значение математического
ожидания соответствующий случайной величины, т.е.
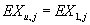 ,
а оценкой этого прогноза – среднее арифметическое по выборке, т.е. ,
а оценкой этого прогноза – среднее арифметическое по выборке, т.е.
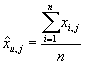 . .
|
(1)
|
Число единиц заказанного j-ого товара входит в эту сумму с одинаковым весом
для каждой i-ой транзакции, что соответствует нашему предположению о равноценности
каждой транзакции. Метод фильтрации по пользователям заключается в том, что мы постулируем,
что более похожие транзакции надо учитывать при прогнозировании с большим весом
в сумме, чем менее похожие. Т.е., суммируя заказы j-ого товара по всем транзакциям
мы должны учитывать вес
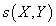 , описывающий степень похожести между двумя транзакциями X и Y. Т.е.
вместо формулы (1) при прогнозировании размера заказа j-товара в u-ой
(новой) транзакции мы используем формулу:
, описывающий степень похожести между двумя транзакциями X и Y. Т.е.
вместо формулы (1) при прогнозировании размера заказа j-товара в u-ой
(новой) транзакции мы используем формулу:
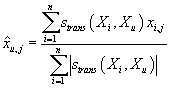 . .
|
(2)
|
Чем больше сходство между транзакциями Xi и Xu,
с тем большим весом входит число заказанного на i-ой транзакции j-ого
товара во взвешенную сумму при прогнозе.
Далее мы рассмотрим версии этого алгоритма в зависимости от способа вычисления функции
близости между транзакциями
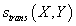 . .
K ближайших соседа
Суть метода состоит в определении K ближайших к данной транзакции транзакций
и использовании среднего значения их рейтингов для прогнозирования неизвестных рейтингов
в данной транзакции. Мерой близости между транзакциями служит какая-либо метрика
на пространстве m-мерных векторов рейтингов товаров, например, индуцированная
евклидовой нормой.
Xu - исследуемая транзакция,
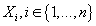 - сохраненная история завершенных транзакций. Будем обозначать матрицей
- сохраненная история завершенных транзакций. Будем обозначать матрицей
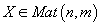 со строками в виде транзакций и столбцами
со строками в виде транзакций и столбцами
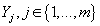 в виде рейтингов товаров. Обозначим
в виде рейтингов товаров. Обозначим
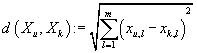 - расстояние между транзакциями. Прогноз j-ого рейтинга в u-ой транзакции
вычисляется как среднее значение j-ого рейтинга в K ближайших к Xu
транзакциях
- расстояние между транзакциями. Прогноз j-ого рейтинга в u-ой транзакции
вычисляется как среднее значение j-ого рейтинга в K ближайших к Xu
транзакциях
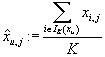 ,
где ,
где
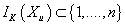 ,
состоит из K ближайших к Xu транзакций. Или, используя
формулу (2), мы можем записать ,
состоит из K ближайших к Xu транзакций. Или, используя
формулу (2), мы можем записать
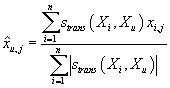 ,
где функция близости определяется как ,
где функция близости определяется как
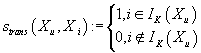 . .
|
(3)
|
Взвешенные ближайшие соседи
Суть метода – использовать для усреднения не только K, а все транзакции,
взятые с весами, отражающими степень близости к исследуемой транзакции.
Как и в прошлом методе Xu - исследуемая транзакция,
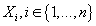 - сохраненная история завершенных транзакций.
- сохраненная история завершенных транзакций.
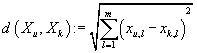 - расстояние между транзакциями.
- расстояние между транзакциями.
Определим веса, отражающие степень близости между транзакциями как величины обратные
расстоянию, т.е.
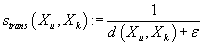 , ,
|
(4)
|
(4) где
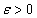 малое число, чтобы гарантировать, что знаменатель нигде не обращается в 0.
Прогноз j-ого рейтинга в u-ой транзакции вычисляется как средневзвешенное
значение j-ого рейтинга по всем транзакциям с весами обратно пропорциональными
расстоянию между транзакциями.
малое число, чтобы гарантировать, что знаменатель нигде не обращается в 0.
Прогноз j-ого рейтинга в u-ой транзакции вычисляется как средневзвешенное
значение j-ого рейтинга по всем транзакциям с весами обратно пропорциональными
расстоянию между транзакциями.
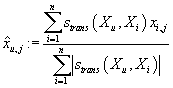
Метрики, основанные на углах между векторами
В качестве степени схожести между транзакциями используется корреляционный коэффициент
Пирсона между m-мерными векторами транзакций (показатель линейной зависимости
между центрированными векторами транзакций)
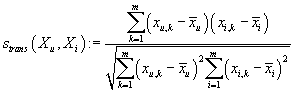
|
(5)
|
или косинус между m-мерными векторами транзакций (показатель линейной зависимости
между векторами транзакций)
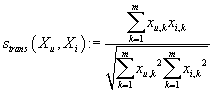 . .
|
(6)
|
Практическое использование показало, что лучшие результаты получаются если при прогнозировании
рейтинга вместо его значения использовать его отклонение от среднего значения по
транзакции, т.е.
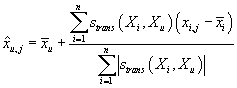 , ,
|
(7)
|
где
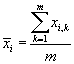 - среднее значение рейтинга по транзакции. Используя (7) мы фактически прогнозируем
отклонение рейтинга j-ого товара от среднего рейтинга по транзакции.
- среднее значение рейтинга по транзакции. Используя (7) мы фактически прогнозируем
отклонение рейтинга j-ого товара от среднего рейтинга по транзакции.
Сложность и ресурсоемкость
Фильтрация по пользователям показывает хорошую точность в практических применениях.
Однако, недостатком всех вариантов приведенного алгоритма является его ресурсоемкость
(требование к памяти) и сложность (количество вычислений, требуемое для получения
рекомендаций). А именно:
- Если хранить в памяти (для быстрого доступа) вектора рейтингов для всех транзакций,
т.е. матрицу n строк на m столбцов, то для среднего интернет-магазина (~1 млн транзакций
и ~10 тыс товаров) потребуется хранить в памяти ~10 млрд действительных чисел (по
8 байт), что представляется невозможным для имеющихся в распоряжении таких магазинов
компьютеров. Осуществлять доступ к этим данным с диска (БД), естественно, возможно,
но это сильно замедляет выполнение операций и, соответственно, повышает требования
к аппаратному обеспечению с точки зрения скорости доступа к дисковому вводу/выводу
и процессору с точки зрения скорости выполнения арифметических операций.
- Каждое сравнение данной транзакции с одной из n остальных занимает порядка O(m)
операций, т.е. всего надо произвести n*O(m) операций для определения степени
похожести данной транзакции с остальными.
- Вычисление рейтинга для каждого из m товаров потребует выполнения порядка
O(n) операций усреднения по транзакциям, т.е. m*O(n) операций для
всех товаров.
- Итого нам потребуется выполнить
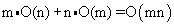 арифметических операций для получения рейтингов всех товаров для данной транзакции
чтобы получить рекомендации.
арифметических операций для получения рейтингов всех товаров для данной транзакции
чтобы получить рекомендации.
Вышеприведенные рассуждения показывают, что фильтрация по пользователям может применяться
только к относительно небольшим базам данных.
Фильтрация по товарам
Идея в фильтрации по товарам состоит в выставлении неизвестного рейтинга товару
в анализируемой транзакции на основании взвешенных рейтингов других товаров, входящих
в эту транзакцию. Рейтинг товара получается тем больше, чем больше рейтинг у других
товаров в анализируемой транзакции, которые обычно покупаются с ним совместно. Т.е.
если мы пытаемся проставить рейтинг товару А и нам уже известен рейтинг товара
Б в этой транзакции, то рейтинг Б будет учитываться в вычислении рейтинга
А с учетом того как часто А и Б входят в одну транзакцию. Мы
получаем формулу, аналогичную (1):
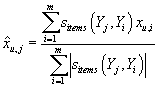 . .
|
(8)
|
Часто вместо абсолютной величины прогноза рейтинга товара прогнозируют отклонение
рейтинга от средней по всем транзакциям для данного товара величину:
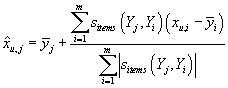 , ,
|
(9)
|
, где
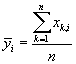 - средний по всем транзакциям рейтинг i-ого товара.
- средний по всем транзакциям рейтинг i-ого товара.
Далее, аналогично фильтрации по пользователям, мы рассмотрим версии этого алгоритма
в зависимости от способа вычисления функции близости между векторами рейтингов товаров
Yj и Yi.
K ближайших соседа
Для j-ого n-мерного вектора рейтингов товара Yj
вычисляются K ближайших в евклидовой норме вектора
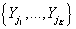 и определяется множество
и определяется множество
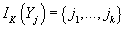 , состоящее из индексов этих K ближайших к Yj соседей.
Тогда степень близости между векторами товаров Yj и Yi
в (8) и (9) определяется как
, состоящее из индексов этих K ближайших к Yj соседей.
Тогда степень близости между векторами товаров Yj и Yi
в (8) и (9) определяется как
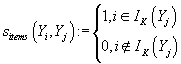 . .
|
(10)
|
Т.е. усреднение в формуле (8) и (9) происходит только по K
ближайшим товарам:
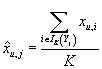 . .
Взвешенные ближайшие соседи
Степень близости между векторами товаров Yj и Yi
в (8) и (9) определяется как величина, обратная евклидовому расстоянию
между ними, т.е.
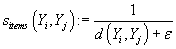 . .
|
(11)
|
Частота попарного вхождения
Весовые коэффициенты, учитывающие «близость» между n-мерными векторами рейтингов
товаров Yj и Yi вычисляются как относительные
частоты совместного вхождения двух товаров в одну транзакцию:
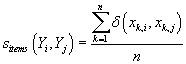 , ,
|
(12)
|
где
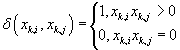 - флаг того, что i-ый и j-ый товар совместно входят в k-ую
транзакцию.
- флаг того, что i-ый и j-ый товар совместно входят в k-ую
транзакцию.
Метрики на основе углов между векторами товаров
В качестве меры близости векторов товаров используется также корреляция Пирсона
или косинус угла между ними:
 , ,
|
(13)
|
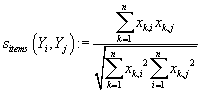 , ,
|
(14)
|
где
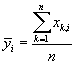 - среднее значение рейтинга по i-ому товару.
- среднее значение рейтинга по i-ому товару.
Сложность и ресурсоемкость
В отличие от алгоритма фильтрации по транзакциям, где вычисление степени близости
анализируемой транзакции ко всем остальным транзакциям может производиться только
в реальном времени, так как данные о текущей транзакции становятся доступными только
в момент выработки рекомендаций, в алгоритме фильтрации по товарам степень близости
анализируемого товара ко всем остальным товарам может быть вычислена в отложенном
режиме по расписанию, так как вектора рейтингов всех товаров доступны до момента
формирования рекомендации. Таким образом, разделив процесс выработки рекомендаций
на отложенную стадию (вычисление степени близости товаров друг к другу) и стадию
в реальном времени (вычисление рейтингов товаров), мы получим, что сложность алгоритма
фильтрации по товарам на стадии формирования рекомендаций равна O(m2),
что в отличие от сложности фильтрации по транзакциям O(mn) не зависит от
числа транзакций. Таким образом, если число транзакций значительно превышает число
товаров, то алгоритм фильтрации по товарам оказывается более эффективным с точки
зрения времени формирования рекомендаций, чем алгоритм фильтрации по транзакциям
благодаря возможности проведения отложенной предобработки данных.
Комбинированная фильтрация
В рассмотренных выше алгоритмах фильтрации по пользователям (взвешенное усреднение
рейтингов по исследуемому товару по похожим транзакциям) и фильтрации по товарам
(взвешенное усреднение рейтингов похожих товаров в исследуемой транзакции) используется
только одна часть информации из накопленных данных для прогнозирования неизвестных
рейтингов (используется или корреляция между векторами транзакций или корреляция
между векторам рейтингов товаров). В этой связи интуитивно представляется желательным
объединить рейтинги как от похожих транзакций, так и от похожих товаров для более
эффективного использования имеющейся информации. Также, рассмотренные выше методы
совместной фильтрации игнорируют информацию, которую можно получить от рейтингов
товаров, похожих на исследуемый товар из других транзакций, похожих на исследуемую
транзакцию. Отказ от использования этих рейтингов уменьшает возможность прогнозирования
из-за недостатка похожих рейтингов. Таким образом, идея комбинированной фильтрации
заключается в получении оценки неизвестного рейтинга как взвешенной суммы оценок
на основании фильтрации по транзакциям, фильтрации по товарам и смешенной фильтрации
(на основании рейтингов похожих товаров в похожих транзакциях).
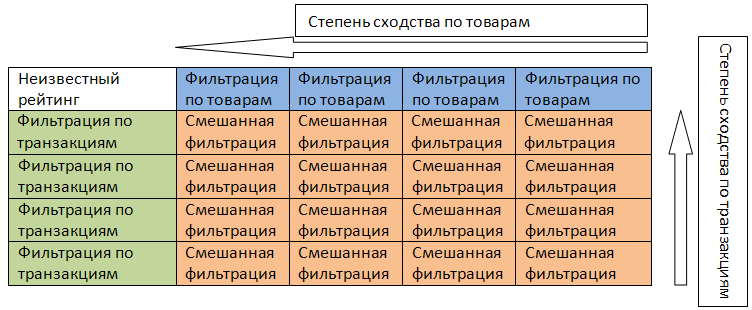
Для получения рейтинга при смешенной фильтрации, т.е. на основании похожих товаров
в похожих транзакциях нам необходимо определить совместную степень сходства между
парами транзакция-товар. Для этой цели используется величина, учитывающая степень
сходства отдельно соответствующих транзакций и отдельно товаров. Комбинированная
степень сходства не превышает отдельных степеней сходства между транзакциями и товарами.
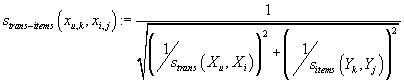 , ,
|
(15)
|
где Strans вычисляется согласно (5) или (6), а Sitems
– согласно (13) или (14).
Введем следующие обозначения: под множеством
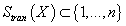 будем обозначать индексы K самых близких с точки зрения (5) или (6)
к X транзакций из
будем обозначать индексы K самых близких с точки зрения (5) или (6)
к X транзакций из
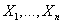 . Под
. Под
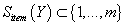 будем обозначать индексы K самых близких с точки зрения (13) или (14)
к Y товара из
будем обозначать индексы K самых близких с точки зрения (13) или (14)
к Y товара из
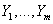 . Сортируя и переиндексируя строки и колонки матрицы рейтингов по степени схожести
к исследуемой транзакции и к исследуемому товару и оставив в ней для последующего
анализа не более K строк и столбцов, мы получим матрицу похожих транзакций
и товаров
. Сортируя и переиндексируя строки и колонки матрицы рейтингов по степени схожести
к исследуемой транзакции и к исследуемому товару и оставив в ней для последующего
анализа не более K строк и столбцов, мы получим матрицу похожих транзакций
и товаров
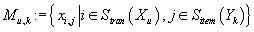 . .
Если для оценки неизвестного рейтинга мы будем учитывать только самый первый столбец
с использованием меры близости по транзакциям, то получим оценку по транзакциям:
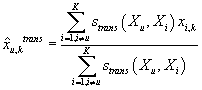 . .
|
(16)
|
Если для оценки неизвестного рейтинга мы будем учитывать только первую строку с
использованием меры близости по товарам, то получим оценку по товарам:
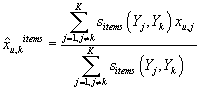 . .
|
(17)
|
Если для оценки рейтинга мы будем учитывать все элементы матрицы кроме первой строки
и первого столбца, т.е. похожие товары, участвующие в похожих транзакциях, то получим
оценку:
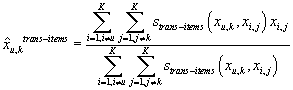 . .
|
(18)
|
Итоговая комбинированная оценка неизвестного рейтинга получается в виде взвешенной
оценки из (16), (17) и (18):
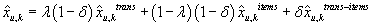 , ,
|
(19)
|
где
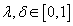 – веса учета соответствующих оценок. При
– веса учета соответствующих оценок. При
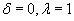 мы получаем фильтрацию по транзакциям, при
мы получаем фильтрацию по транзакциям, при
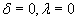 – фильтрацию по товарам, при
– фильтрацию по товарам, при
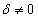 мы также учитываем рейтинги сходных товаров из сходных транзакций.
мы также учитываем рейтинги сходных товаров из сходных транзакций.
Понижение размерности
Как уже было отмечено, основным недостатком алгоритмов совместной фильтрации является
необходимость выполнения большого количества операций для вычисления степени похожести
товаров или транзакций и для усреднения рейтингов по товарам или по транзакциям
при прогнозировании неизвестного рейтинга. Для уменьшения трудоемкости операций
усреднения (т.е. в формулах (2), (8)) на практике используется не
усреднение по всем транзакциям (2) и не по всем товарам (8), а лишь
по K наиболее похожим. Численные эксперименты с реальными базами данных ([4])
показали, что выбор числа K наиболее похожих транзакций или товаров, по которым
производится усреднение для вычисления рейтинга, оказывает сильное влияние на точность
рекомендаций. Общей тенденцией является увеличение точности при начальном увеличении
числа K, а затем, после достижения максимума, точность стабилизируется или
плавно ухудшается. Ухудшение точности при дальнейшем увеличении K объясняется
тем фактом, что все большее количество «непохожих» транзакций или товаров принимается
к рассмотрению. Оптимальное число K для фильтрации по товарам в среднем имеет
значение около 10, в то время как по транзакциям – на порядок больше. Таким образом
рассмотрение только K ближайших транзакций или товаров вместо всех имеющихся
в распоряжении не только ускоряет процесс вычисления неизвестного рейтинга, но и
увеличивает точность прогноза.
Для уменьшения сложности вычисления степени схожести векторов товаров или транзакций
(например, в формулах (5) или (13)) используется подход понижения
размерности матрицы транзакций-товаров, основанный на разложении этой матрицы по
сингулярным значениям. Разложение по сингулярным значениям (SVD – Singular Value
Decomposition) представляет собой представление матрицы
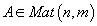 с рангом
с рангом
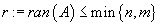 в виде
в виде
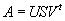 , где матрицы
, где матрицы
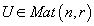 и
и
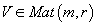 состоят из ортонормальных столбцов, являющихся собственными векторами при ненулевых
собственных значениях матриц AAt и AtA соответственно,
а
состоят из ортонормальных столбцов, являющихся собственными векторами при ненулевых
собственных значениях матриц AAt и AtA соответственно,
а
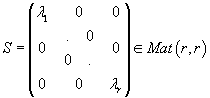 - диагональная матрица с положительными диагональными элементами
- диагональная матрица с положительными диагональными элементами
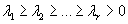 , отсортированными в порядке убывания. Диагональные элементы матрицы S
, отсортированными в порядке убывания. Диагональные элементы матрицы S
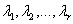 представляют собой собственные значения, соответствующие ненулевым собственным векторам
AAt и AtA (столбцам U и V). Столбцы
матрицы U представляют собой, таким образом, ортонормальный базис пространства
столбцов матрицы A, а столбцы матрицы V – ортонормальный базис пространства
строк матрицы A. Важным свойством SVD-разложения является тот факт, что если
для d<r преобразовать матрицу S в матрицу
представляют собой собственные значения, соответствующие ненулевым собственным векторам
AAt и AtA (столбцам U и V). Столбцы
матрицы U представляют собой, таким образом, ортонормальный базис пространства
столбцов матрицы A, а столбцы матрицы V – ортонормальный базис пространства
строк матрицы A. Важным свойством SVD-разложения является тот факт, что если
для d<r преобразовать матрицу S в матрицу
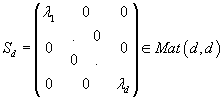 , состоящую только из d наибольших диагональных элементов, а также оставить
в матрице U и V только d первых столбцов, т.е. преобразовать
их в
, состоящую только из d наибольших диагональных элементов, а также оставить
в матрице U и V только d первых столбцов, т.е. преобразовать
их в
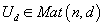 и
и
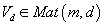 , то матрица
, то матрица
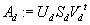 будет являться лучшей аппроксимации матрицы A относительно нормы Фробениуса
среди всех матриц с рангом d, т.е.
будет являться лучшей аппроксимации матрицы A относительно нормы Фробениуса
среди всех матриц с рангом d, т.е.
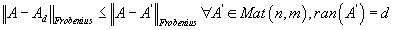 . .
Суть понижения размерности при помощи SVD-разложения исходной матрицы транзакций-товаров
A состоит в следующем: сначала строится разложение
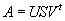 , затем для фиксированного выбранного d<<ran(A) мы получаем лучшую
d-ранговую аппроксимацию матрицы A в форме
, затем для фиксированного выбранного d<<ran(A) мы получаем лучшую
d-ранговую аппроксимацию матрицы A в форме
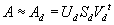 .
.
В случае фильтрации по товарам каждый j-ый столбец Yj матрицы
A, соответствующий рейтингам j-ого товара, аппроксимируется j-ым
столбцом матрицы Ad, который представляет собой проекцию вектора
Yj на пространство, образованное d ортонормальными столбцами
матрицы Ud с коэффициентами разложения
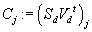 , соответствующими j-ому d-мерному вектору-столбцу матрицы
, соответствующими j-ому d-мерному вектору-столбцу матрицы
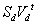 . Таким образом, вместо n-мерного вектора j-ого товара Yj
мы рассматриваем d-мерный вектор Cj, представляющий собой
вектор коэффициентов разложения проекции Yj по базису Ud.
Используя описанный подход, для определения степени похожести векторов товаров Yu
и Yk мы вычисляем степень похожести их d-мерных аппроксимаций,
т.е. вычисляем, например, косинусы между векторами коэффициентов Cu
и Ck разложения исходных векторов товаров Yu
и Yk по базису Ud в виде, аналогичном (14):
. Таким образом, вместо n-мерного вектора j-ого товара Yj
мы рассматриваем d-мерный вектор Cj, представляющий собой
вектор коэффициентов разложения проекции Yj по базису Ud.
Используя описанный подход, для определения степени похожести векторов товаров Yu
и Yk мы вычисляем степень похожести их d-мерных аппроксимаций,
т.е. вычисляем, например, косинусы между векторами коэффициентов Cu
и Ck разложения исходных векторов товаров Yu
и Yk по базису Ud в виде, аналогичном (14):
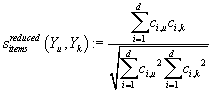 . .
|
(20)
|
В отличии от (14) нам требуется O(d) операций для вычисления степени
похожести между векторами товаров вместо O(n), что значительно ускоряет вычисления
при d<<n.
Неизвестный рейтинг прогнозируется по формуле, аналогичной (8), но вместо
исходных рейтингов Xu,i в ней участвуют элементы
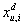 из аппроксимирующей матрицы Ad
из аппроксимирующей матрицы Ad
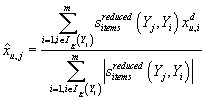 . .
|
(21)
|
Аналогично, в случае фильтрации по транзакциям, каждая i-ая строка матрицы
A, соответствующая i-ой транзакции, аппроксимируется i-ой строкой
матрицы Ad, которая представляет собой линейную комбинацию ортонормальных
строк матрицы
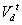 с коэффициентами, соответствующими d-мерной i-ой строке
с коэффициентами, соответствующими d-мерной i-ой строке
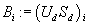 матрицы
матрицы
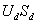 .
Т.е. вместо определения степени похожести m-мерных векторов транзакций Xu
и Xk мы сравниваем d-мерные коэффициенты их разложения
Bu и Bk по базису строк матрицы .
Т.е. вместо определения степени похожести m-мерных векторов транзакций Xu
и Xk мы сравниваем d-мерные коэффициенты их разложения
Bu и Bk по базису строк матрицы
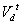 . Вместо, например, (6) мы получаем:
. Вместо, например, (6) мы получаем:
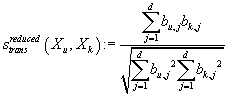 . .
|
(22)
|
В отличие от (6) нам потребуется не O(m) операций, а O(d),
что значительно ускоряет вычисления при d<<m.
Неизвестный рейтинг прогнозируется по формуле, аналогичной (2), но вместо
исходных рейтингов Xu,i в ней участвуют элементы
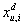 из аппроксимирующей матрица Ad
из аппроксимирующей матрица Ad
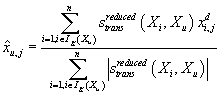 . .
|
(23)
|
В [4] было показано, что ранг матрицы аппроксимации d оказывает большое
значение на точность получаемого прогноза. Это число должно быть достаточно маленьким,
чтобы оказать заметное воздействие на ускорение выполнения вычислений и чтобы минимизировать
переобучение с одной стороны, и достаточно большим, чтобы содержать важные объективные
взаимосвязи между транзакциями и товарами, содержащимися в исходных данных. Точность
прогнозирования следует следующему правилу: при увеличении числа d точность
прогноза растет и быстро достигает своего максимума (в среднем около d=6),
а затем точность ухудшается. Причина ухудшения точности прогноза при увеличении
ранга аппроксимирующей матрицы объясняется переобучением (излишним усложнением)
модели, ведущим не к выявлению объективных зависимостей между товарам и транзакциями,
а к подгонке к обучающим данным.
Таким образом, использование только ограниченного числа наиболее похожих товаров
и транзакций, а также аппроксимация матрицы транзакций-товаров матрицей значительно
меньшего ранга не только упрощает вычисления, но и увеличивает точность прогнозирования
из-за уменьшения влияния факторов переобучения модели.
Метод персональной диагностики
Описание метода персональной диагностики (PD) основано на работе [5]. Суть
метода заключается в том, что мы рассматриваем анализируемую транзакцию Xu
как-будто она была выбрана случайно с равномерным распределением из генеральной
совокупности
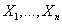 транзакций с добавлением белого гауссовского шума. Т.е. помимо наблюдаемой случайной
величины Xu, соответствующей рейтингам товаров в анализируемой
транзакции, у нас есть еще ненаблюдаемая случайная величина
транзакций с добавлением белого гауссовского шума. Т.е. помимо наблюдаемой случайной
величины Xu, соответствующей рейтингам товаров в анализируемой
транзакции, у нас есть еще ненаблюдаемая случайная величина
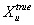 , которая описывает вариантом какой транзакции является Xu на
«самом деле». Величина
, которая описывает вариантом какой транзакции является Xu на
«самом деле». Величина
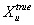 может принимать значения
может принимать значения
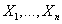 с вероятностью
с вероятностью
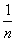 (если все вектора транзакций попарно различны). Ее можно также интерпретировать
как флаг принадлежности к типу пользователя или к одноэлементному кластеру, соответствующему
каждой транзакции. Итак, априорная вероятность принадлежности u-ой транзакции
к i-ому типу пользователя принимается равной
(если все вектора транзакций попарно различны). Ее можно также интерпретировать
как флаг принадлежности к типу пользователя или к одноэлементному кластеру, соответствующему
каждой транзакции. Итак, априорная вероятность принадлежности u-ой транзакции
к i-ому типу пользователя принимается равной
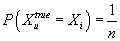 . .
|
(24)
|
Условная плотность распределение рейтинга k-ого товара в u-ой транзакции
при известном значении «истинного» значения рейтинга k-ого товара в u-ой
транзакции (или рейтинга k-ого товара для транзакции, вариантом которой u-ая
транзакция является на «самом деле») принимается нормальной с математическим ожиданием,
равным рейтингу «истинной» транзакции и с дисперсией
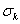 , являющейся свободным параметром:
, являющейся свободным параметром:
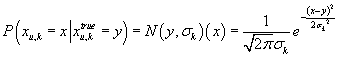 . .
|
(25)
|
Кроме того, при фиксированном известном значение «истинного» рейтинга k-ого
товара в u-ой транзакции (рейтинга k-ого товара в транзакции, вариантом
которой является u-ая трназакция), случайная величина наблюдаемого рейтинга
k-ого товара в u-ой транзакции не зависит условно ни от одной случайной
величины в модели, т.е.
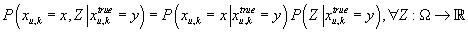 . .
|
(26)
|
На основании этого условная плотность вероятности рейтинга k-ого товара в
u-ой транзакции при известных значениях некоторого набора рейтингов других
товаров в этой транзакции равна:
Далее получаем:
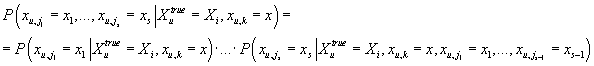
|
(28)
|
Из условной независимости (26) получаем из (28):
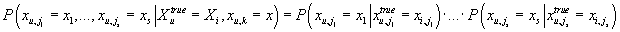
Аналогично:
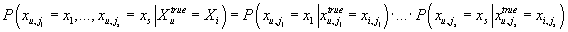
После подстановки двух последних равенств в (27) и учитывая (24),
получаем:
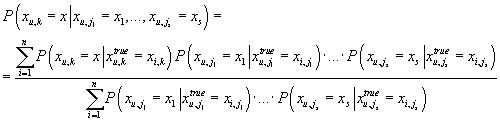
|
(29)
|
С учетом (25) получаем из (29):
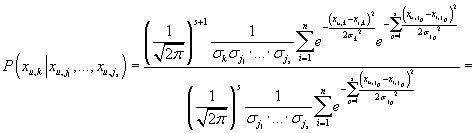
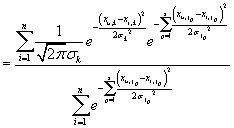
|
(30)
|
Для краткости обозначим
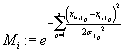
|
(31)
|
Прогнозом неизвестного рейтинга xu,k мы будем считать его условное
математическое ожидание с учетом известных значений рейтингов, т.е.
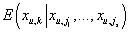 , т.к. именно эта величина является лучшей аппроксимацией с точки зрения L2-нормы
случайной величины Xu,k в пространстве измеримых функций от
, т.к. именно эта величина является лучшей аппроксимацией с точки зрения L2-нормы
случайной величины Xu,k в пространстве измеримых функций от
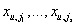 (т.е. среди функций от имеющейся информации). Зная условную плотность xu,k
из (30) мы можем вычислить прогноз.
(т.е. среди функций от имеющейся информации). Зная условную плотность xu,k
из (30) мы можем вычислить прогноз.
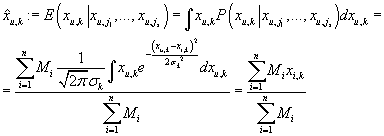
|
(32)
|
Т.е.
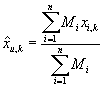
|
(33)
|
Таким образом метод персональной диагностики представляет собой разновидность метода
фильтрации по транзакциям (формулы (33) и (2) идентичны), в котором
в качестве меры близости между транзакциями принимается значение из формулы (31),
т.е.
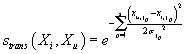
|
(34)
|
Описанный метод интересен тем, что имеет в качестве основы ясную теоретико-вероятностную
модель.
Нормализация исходных данных
Часто исходная матрица рейтингов нормализуется: строки и столбцы приводятся к векторам
с нулевым средним. Сначала мы нормализуем матрицу, вычитая средние рейтинг по товарам:
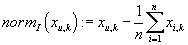 , далее мы преобразуем полученную матрицу, вычитая из нее средние значения по транзакциям:
, далее мы преобразуем полученную матрицу, вычитая из нее средние значения по транзакциям:
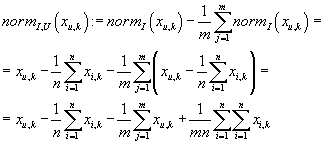 . .
Далее везде вместо элементов Xu,k мы используем нормализованные
элементы
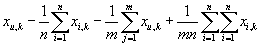
|
(35)
|
Алгоритмы, основанные на моделях
В отличие от ранее рассмотренной совместной фильтрации, оперирующей надо всей базой
данных для создания рекомендаций (Memory-based), алгоритмы, основанные на моделях
(Model-based) используют базу данных для обучения или настройки модели, которая
затем используется при составлении рекомендаций. В процессе обучения модели вычисляется
классификационная функция, которая в зависимости от имеющихся в распоряжении рейтингов
позволяет получить значения неизвестных рейтингов. Вид классификационной функции
(модель) обновляется регулярно по расписанию для учета всех новых поступивших транзакций,
например , в периоды наименьшей загрузки вычислительных ресурсов. Разбиения процесса
на отложенное периодическое обучение (ресурсоемкое вычисление и сохранение значений
параметров и структуры модели) и прогнозирование рейтингов в реальном времени (относительно
незатратное) позволяет оптимизировать время выполнения операций. К тому же полученная
модель данных имеет самостоятельную ценность кроме возможности прогнозирования так
как позволяет получить описательный анализ имеющихся данных и зависимостей в них.
Упрощенный алгоритм Байеса (Naive Bayes)
Пусть значения рейтингов могут принимать одно из конечного набора значений
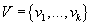 . .
. Тогда условная вероятность, того что в u-ой транзакции рейтинг j
-ого товара будет vj при условии, что некое подмножество других
товаров имеет заданный набор значений рейтингов в данной транзакции будет равна:
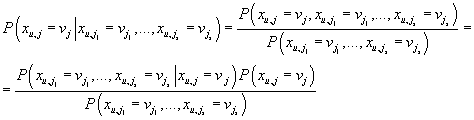 . .
|
(36)
|
Оптимальная (с точки зрения минимизации вероятности принятия неправильного решения)
решающая функция
 имеет вид
имеет вид
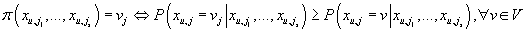 , ,
|
(37)
|
т.е. на основании имеющегося неполного набора
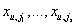 проставленных рейтингов мы принимаем решение, что отсутствующий рейтинг Xu,j
принимает значение vj тогда и только тогда, когда условная вероятность
этого рейтинга для Xu,j при известном частичном наборе
проставленных рейтингов мы принимаем решение, что отсутствующий рейтинг Xu,j
принимает значение vj тогда и только тогда, когда условная вероятность
этого рейтинга для Xu,j при известном частичном наборе
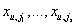 максимальна.
максимальна.
Упрощенность данного подхода состоит в дополнительном допущении об условной независимости
двух любых рейтингов при условии третьего, т.е.:
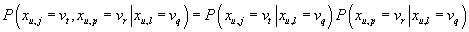 . .
|
(38)
|
С учетом (38) мы можем переписать (36) как
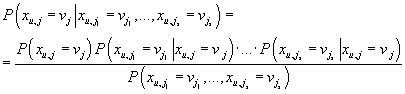 . .
|
(39)
|
Знаменатель в правой части (39) не зависит от vj, т.е.
для нахождения максимума условной вероятности по vj в левой части
(39) надо найти максимум числителя правой части по vj.
Т.е. мы принимаем решение, что
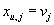 при условии
при условии
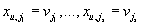 тогда и только тогда, когда
тогда и только тогда, когда
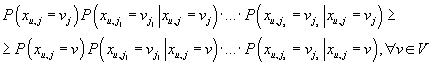 . .
|
(40)
|
Оценка максимального правдоподобия для вероятностей и условных вероятностей в (40)
соответствует частотам соответствующих событий в данных. Т.е.
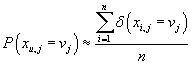
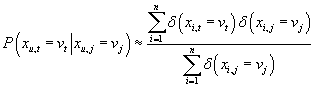 , ,
|
(41)
|
где
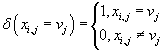 . .
Из (40) и (41) следует, что мы принимаем решение
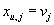 при условии
при условии
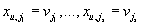 тогда и только тогда, когда
тогда и только тогда, когда
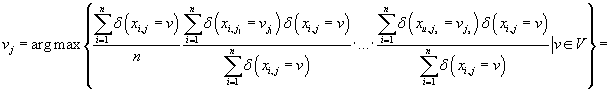
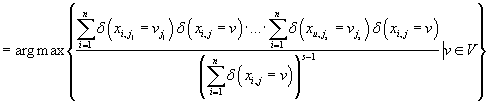 . .
|
(42)
|
Если оценки безусловных и условных вероятностей из (41) получать по расписанию
(например, ночью) и сохранять в базе данных, то для генерации рейтингов для одной
транзакции в online режиме по формуле (42) потребуется O(V*m)
арифметических операций, что не зависит от числа накопленных транзакций. Таким образом,
разбиения процесса рекомендаций на отложенное периодическое обучение (вычисление
и сохранение значений параметров ) и прогнозирование рейтингов в реальном времени
позволяет оптимизировать время выполнения операций.
Кластеризация по транзакциям (пользователям)
Идея этого подхода заключается в группировке транзакций по входящим в них товарам,
а затем вычисления неизвестного рейтинга в исследуемой транзакции как наиболее вероятного
в группе (кластере), к которой эта транзакция принадлежит с наибольшей вероятностью.
Разбиение множества транзакций на кластеры осуществляется по расписанию каким-либо
методом кластеризации Data Mining (K-Means, Expectation Maximization и др.). Определения
принадлежности к кластеру и значений неизвестных рейтингов товаров в исследуемой
транзакции производится в реальном времени.
Сама идея аналогична методу K ближайших соседей, в котором для исследуемой
транзакции мы определяли K наиболее похожих на нее транзакций, а рейтинги
вычислялись как наиболее вероятные среди этих K элементов. Разница с кластеризацией
по транзакциям заключается в том, что в последнем алгоритме кластеры вычисляются
заранее, а не для каждой исследуемой транзакции в реальном времени, поэтому кластеризация
по транзакциям работает значительно быстрее, но менее точно, так как для каждого
товара множество вариантов возможных рекомендаций ограничивается небольшим количеством
кластеров.
Байесовская кластеризация по товарам и пользователям
Идея этого метода основывается на работе [8] и заключается в следующем:
- Существует отдельный набор групп пользователей и отдельный набор групп товаров,
вхождение в которые определяют значение рейтинга. Т.е. пользователи из группы i
оценивают товары из группы j примерно одинаково.
- Пользователь или товар могут входить в несколько групп. Т.е. фильм может быть историческим,
военным и психологическим одновременно.
Пусть пространство событий представляет собой подмножества из множества кортежей
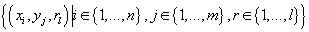 , случайная величина X принимает одно из значений
, случайная величина X принимает одно из значений
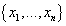 множества пользователей, случайная величина Y принимает одно из значений
множества пользователей, случайная величина Y принимает одно из значений
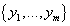 множества товаров, а случайная величина R принимает одно из значений
множества товаров, а случайная величина R принимает одно из значений
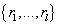 множества возможных рейтингов. Т.е. множество элементарных событий – тройки пользователь,
товар, рейтинг. Пусть также имеются ненаблюдаемые случайные величины: C принимает
одно из значений
множества возможных рейтингов. Т.е. множество элементарных событий – тройки пользователь,
товар, рейтинг. Пусть также имеются ненаблюдаемые случайные величины: C принимает
одно из значений
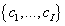 множества классов пользователей и D принимает одно из значений
множества классов пользователей и D принимает одно из значений
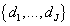 множества классов товаров. Условная независимость случайных величин X, Y, R, C, D
пусть описывается следующей Байесовской сетью:
множества классов товаров. Условная независимость случайных величин X, Y, R, C, D
пусть описывается следующей Байесовской сетью:
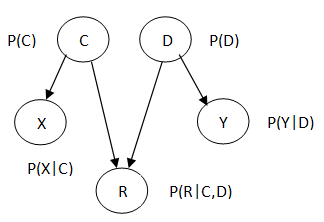
Т.е. рейтинг непосредственно зависит только от групп, в которые входят пользователь
и товар. Таким образом, совместное распределение вероятностей имеет вид:
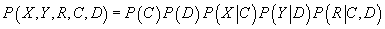
|
(43)
|
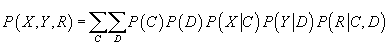
|
(44)
|
Задача оценки неизвестных параметров
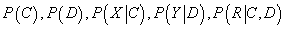 определяется известным методом кластеризации – Expectation Maximization (EM). Суть
метода заключается в итеративном выполнении двух шагов:
определяется известным методом кластеризации – Expectation Maximization (EM). Суть
метода заключается в итеративном выполнении двух шагов:
- Шаг E: вычисление новой апостериорной вероятности вхождения в кластеры при помощи
(43) и (44), где
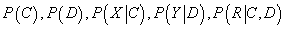 определены на прошлом шаге M или заданы произвольно на первом шаге:
определены на прошлом шаге M или заданы произвольно на первом шаге:
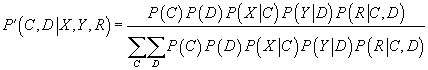
|
(45)
|
- Шаг M: новые параметры
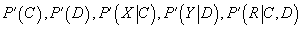 вычисляются по формулам, полученным при решении задачи максимизации логарифма функции
правдоподобия, при фиксированном значении
вычисляются по формулам, полученным при решении задачи максимизации логарифма функции
правдоподобия, при фиксированном значении
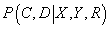 , полученном на прошлом шаге E.
, полученном на прошлом шаге E.
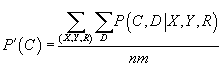
|
(46)
|
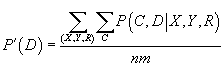
|
(47)
|
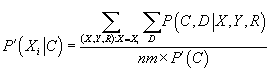
|
(48)
|
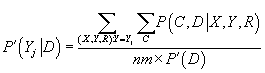
|
(49)
|
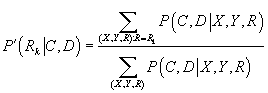
|
(50)
|
Алгоритм EM гарантирует монотонный рост функции правдоподобия, но не исключает возможность
схождения в точке локального, а не глобального максимума, поэтому он выполняется
несколько раз при различных начальных значениях параметров.
После выполнения алгоритма EM мы получаем оценку параметров модели
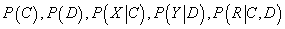 , что позволяет нам рассчитать прогноз неизвестного рейтинга товара Y нового
пользователя
, что позволяет нам рассчитать прогноз неизвестного рейтинга товара Y нового
пользователя
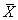 как условное математическое ожидание
как условное математическое ожидание
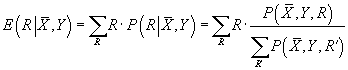
|
(51)
|
В формуле (51) мы используем выражение (44)
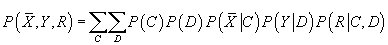 , в котором в правой части все параметры нам известны кроме
, в котором в правой части все параметры нам известны кроме
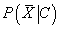 , т.к. пользователь
, т.к. пользователь
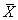 - новый и этот параметр для него не был рассчитан. Для его вычисление еще раз выполняется
алгоритм кластеризации EM со всеми фиксированными значениями параметров кроме
- новый и этот параметр для него не был рассчитан. Для его вычисление еще раз выполняется
алгоритм кластеризации EM со всеми фиксированными значениями параметров кроме
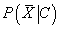 . .
Ассоциативные правила
Выявление ассоциативных правил – это процесс определения частых наборов товаров,
приобретаемых совместно в транзакциях. На основании этих частых наборов формируются
правила вида «если А и Б, то В с вероятностью х». На
основании сформированных правил рекомендуются (проставляются рейтинги) товарам,
которые встречаются в правой части правил, если товары из левой части уже есть в
транзакции. Таким образом, подход, основанный на ассоциативных правилах аналогичен
фильтрации по товарам (рекомендуются товары, которые часто приобретаются совместно
с уже заказанными товарами) особенно в варианте «частоты попарного вхождения». Разница
заключаются в том, что в алгоритме ассоциативных правил, правила формируются в отложенном
режиме по расписанию, а поиск рекомендаций осуществляется в реальном времени на
основании уже полученных правил. В фильтрации по товарам мы вычисляем веса, описывающие
частоту попарного вхождения для каждого вектора товара в реальном времени в процессе
формирования рекомендаций, что значительно более трудоемко. С другой стороны, недостатком
алгоритма ассоциативных правил является то, что не для каждого набора заказанных
товаров в анализируемой транзакции существует правило с достаточной поддержкой и
достоверностью. Так, например, для существования правил вида «А, Б
-> В» для каждой пары товаров А и Б необходимо существование
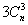 частых набора (существует
частых набора (существует
 подмножеств из 3 элементов в множестве из n элементов, для каждого подмножества
из 3 элементов можно сформировать 3 правила в зависимости от того, какой элемент
будет в правой части этого правила). Для n=1000, число частых наборов в этом
случае должно быть 498 501 000, что при ограничении на частоту набора в 10 транзакций
приводит к необходимости хранения не меньше 5 млрд транзакций, что является очень
серьезным требованием. Эта проблема решается поиском правил, содержащих только один
элемент в левой части, т.е. типа «если А, то Б», для каждого товара
А уже имеющегося в транзакции. Полученным правым частям проставляется рейтинг
в зависимости от вероятности правила. Этот подход еще в большей степени соответствует
фильтрации по товарам с мерой близости векторов товаров в виде частоты попарного
вхождения.
подмножеств из 3 элементов в множестве из n элементов, для каждого подмножества
из 3 элементов можно сформировать 3 правила в зависимости от того, какой элемент
будет в правой части этого правила). Для n=1000, число частых наборов в этом
случае должно быть 498 501 000, что при ограничении на частоту набора в 10 транзакций
приводит к необходимости хранения не меньше 5 млрд транзакций, что является очень
серьезным требованием. Эта проблема решается поиском правил, содержащих только один
элемент в левой части, т.е. типа «если А, то Б», для каждого товара
А уже имеющегося в транзакции. Полученным правым частям проставляется рейтинг
в зависимости от вероятности правила. Этот подход еще в большей степени соответствует
фильтрации по товарам с мерой близости векторов товаров в виде частоты попарного
вхождения.
Выбор критерия сравнения алгоритмов
Проблема выбора подходящего параметра измерения точности осложняется огромным разнообразием
параметров, которые использовались для количественной оценки точности работы РС-систем
в опубликованных исследованиях. Отсутствие стандартизации в этом вопросе наносит
вред прогрессу в этой области знаний, относящейся к развитию рекомендационных систем
на базе совместной фильтрации. Не имея стандартного параметра в качестве меры точности
в этой сфере, исследователи продолжают вводить новые единицы измерения для оценки
своих систем. При таком разнообразии используемых оценочных параметров становится
сложно сравнивать результаты одного опубликованного исследования с результатами
другого. В результате, становится тяжело интегрировать эти разные публикации в единое
целое, чтобы выработать какие-либо общие знания и понятия относительно качества
работы алгоритмов РС.
Растёт понимание того, что хорошая точность рекомендаций сама по себе не удовлетворяет
потребности пользователей РС-системы и не характеризует эффективность её работы.
РС-системы должны предоставлять не только точные, но и полезные рекомендации. Например,
РС-система могла бы достичь высокой точности исключительно за счёт формирования
прогнозов для легко предсказуемых объектов, но это те объекты, относительно которых
пользователи менее всего нуждаются в рекомендациях. Далее, система, которая всегда
рекомендует очень популярные объекты, может гарантировать, что пользователям понравится
большая часть рекомендуемых объектов, но простой показатель популярности мог бы
делать то же самое.
Точность
Тестирование на точность заключается в случайном разделении транзакций на обучающее
и тестовое множество (в пропорции 90%-10%, 80%-20%). Транзакции в обучающем множестве
служат для оценки рейтингов товаров из транзакций из тестового множества. Товары
из каждой тестовой транзакции случайно разделяются на две группы: «известные» и
«неизвестные». На основании рейтингов группы «известных» товаров строятся рейтинги
для группы «неизвестных» товаров на основании данных из множества обучающих транзакций.
В качестве меры точности прогноза служит средняя абсолютная ошибка прогноза рейтингов
MAE (Mean Absolute Error):
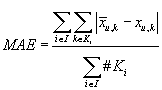
|
(52)
|
где I – индексы тестового множества транзакций, а Ki -
множество «неизвестных» товаров в каждой тестовой транзакции.
Покрытие
Покрытие (зона действия, охват) рекомендательной системы – это измерение области
объектов в системе, по которым РС может формировать прогнозы или выдавать рекомендации.
Системы с низким покрытием могут быть менее значимы для пользователей, так как они
будут ограничены в принятии решений только теми из них, в которых РС будут способны
им помочь. Общепринятой мерой покрытия является доля от общего числа объектов, для
которых могут быть выработаны прогнозы. Самый простой способ измерить покрытие такого
рода – это выбрать произвольную выборку пар пользователь/объект, запросить прогноз
для каждой пары и измерить процент тех, в отношении которых был сделан прогноз.
Покрытие должно замеряться в комбинации с точностью, так чтобы РС-системы не склонялись
к увеличению покрытия за счёт выработки фиктивных прогнозов для каждого объекта.
Скорость обучаемости системы
Рекомендательные системы на основе совместной фильтрации имеют в своём составе алгоритмы
по самообучению, которые функционируют на статистических моделях. В результате,
результаты их работы варьируются в зависимости от объёма доступной для обучения
информации. По мере увеличения количества обучающей информации качество прогнозов
или рекомендаций должно расти. Различные алгоритмы выработки рекомендаций могут
достичь приемлемого качества рекомендаций с разной скоростью. Некоторым алгоритмам
может понадобиться только небольшой объём информации, чтобы начать вырабатывать
приемлемые рекомендации, в то время как другим может понадобиться достаточной большой
объём. В РС-системах рассматривается 3 разных скорости накопления знаний: общая
скорость обучаемости, скорость обучаемости по 1 объекту, и скорость обучаемости
по 1 пользователю.
Общая скорость обучаемости РС-системы – это качество рекомендаций, выраженное как
функция от общего числа рейтингов в системе (или общего числа пользователей системы).
Скорость обучаемости по объекту – это качество рекомендаций относительно определённого
объекта, выраженное как функция от числа рейтингов, имеющихся у определённого объекта.
Также, скорость обучаемости по 1 пользователю – это качество рекомендаций для определённого
пользователя, выраженное как функция от числа рейтингов, который конкретный пользователь
ввёл в систему.
Степень новизны
Можно представить себе РС-систему, выдающую очень точные рекомендации и имеющую
достаточное покрытие, и тем не менее бесполезную для практических целей. Например,
РС система овощного магазина может предлагать купить картошку любому покупателю,
который ее ещё не выбрал. Статистически такая РС высоко точна: почти все покупают
картошку. Однако, каждый приходящий в овощной магазин в прошлом покупал картошку
и знает, хочет он или нет купить её ещё. Далее, менеджеры овощного магазина уже
знают, что картошка пользуется спросом , и они уже так организовали выкладку товара
в своём магазине, чтобы покупатели не смогли мимо неё пройти. Таким образом, чаще
всего покупатель уже принял конкретное решение не покупать картошку во время этого
захода в магазин, и следовательно проигнорирует рекомендацию относительно неё. Более
ценна была бы рекомендация по поводу, например, замороженных овощей, о которых покупатель
ещё не слышал, но которые бы ему понравились. Это пример рекомендаций, которые не
прошли тест на очевидность. Очевидные рекомендации имеют 2 недостатка: 1) покупатель,
заинтересованный в этих товарах, уже их приобрёл; 2) менеджерам магазина не нужны
РС-системы, сообщающие им, какие товары в целом популярны. Они уже инвестировали
средства в организацию своего магазина таким образом, чтобы такие товары были легко
доступны покупателям.
Для анализа РС-систем нужны новые координаты измерений, учитывающие «неочевидность»
рекомендаций. Один из таких параметров – степень новизны. Другой имеющий отношение
к этому параметр – способность к неожиданным открытиям. Рекомендация о случайно
возникшем объекте помогает пользователю найти интересный объект, который иначе он
не смог бы обнаружить. Яркий пример разницы между новизной и способностью к неожиданным
открытиям: рассмотрим РС-систему, которая просто рекомендует фильмы, поставленные
самым любимым режиссёром пользователя. Если система рекомендует фильм, о котором
пользователь ничего не знает – этот фильм является для пользователя новинкой, но
очевидно не неожиданным приятным открытием. Пользователь скорее всего обнаружил
бы этот фильм сам. С другой стороны, РС-система, которая рекомендует фильм нового
режиссёра, скорее всего предоставляет неожиданно интересную рекомендацию. Рекомендации,
являющиеся неожиданно интересными, также по определению являются новинками. Это
различие между способностью системы выдавать рекомендации по новым неизвестным пользователю
объектам и тем из них, что могут оказаться неожиданно интересными, важно при оценке
алгоритмов РС-систем, основанных на методе коллаборативной фильтрации.
Разработать параметр, которым можно будет измерить способность системы выдавать
рекомендации по неожиданно интересным объектам, очень сложно, так как это показатель
того, насколько хорошо рекомендации представляют объекты, являющиеся для пользователей
как привлекательными, так и удивительными. Фактически, обычные методы измерения
качества работы системы прямо противоположны этому.
Поддержка и доверительность прогноза
Пользователи РС-систем часто сталкиваются с проблемой в определении того, как интерпретировать
рекомендации по двум часто конфликтующим показателям. Первый параметр – это поддержка
(support) рекомендации, т.е. насколько по мнению РС-системы пользователю понравится
тот или иной объект. Такие рекомендация основываются на больших массивах данных,
т.е. основываются на шаблонах, присутствующих у большинства пользователей. Второй
параметр – доверительность (confidence) рекомендации, т.е. насколько сильно РС-система
уверена в точности своих рекомендаций. Этот показатель основывается на вероятности
выполнения рекомендуемого действия в зависимости от уже совершенных пользователем
действиях. Эта вероятность может быть велика, но основываться на небольшом числе
случаев, т.е. на неком редком паттерне.
Чтобы помочь пользователям принять эффективное решение на основе рекомендаций, РС-системы
должны помогать пользователям сориентироваться одновременно и по поддержке рекомендаций,
и по доверительности. На практике применяются различные подходы. Системы e-commerce
часто отказываются предоставлять рекомендации, основанные на информационных массивах,
считающихся небольшими. Они хотят рекомендации, на которые пользователи могли бы
положиться. В то же время для выявления неожиданных шаблонов и закономерностей используются
рекомендации, основанные на редких случаях, но обладающие высокой условной вероятностью.
Оценка степени достижения объективных целей
Для любой задачи должна быть разработана соответствующая метрика, которая определяет,
что может считаться успешным итогом (результатом) работы системы. С точки зрения
бизнеса целью может быть повышение прибыли интернет-магазина, посещаемости сайта
и т.п. Если смотреть с позиции системы, то основным показателем качества её работы
может быть точность. Однако с позиции пользователя, параметры качества работы системы
должны устанавливаться в соответствии с их конкретными задачами.
При оценивании степени достижения цели с точки зрения пользователя используются
явные и неявные оценки. Основное отличие – когда у пользователей в явной форме спрашивается
об их реакции на работу системы и когда ведётся наблюдение за их поведением. Первый
тип оценки обычно использует методы интервьюирования и опроса. Второй тип обычно
включает в себя ведение лога (протокола) пользовательского поведения, который впоследствии
становится предметом различного рода анализов.
Литература
- J. Herlocker, J. Konstan, L. Terveen, and J. Riedl. «Evaluating collaborative filtering
recommender systems», ACM Translations on Information Systems, Vol. 22(1), 2004.
Jun Wang, Arjen P. de Vries, Marcel J.T. Reinders, «Unifying Userbased and
Itembased Collaborative Filtering Approaches by Similarity Fusion».
- Justin Basilico, Thomas Hofmann «Unifying Collaborative and Content-Based Filtering».
- Manolis G. Vozalis, Konstantinos G. Margaritis «Applying SVD on Generalized Item-based
Filtering».
- David M. Pennock, Eric Horvitz, Steve Lawrence and C. Lee Giles «Collaborative Filtering
by Personality Diagnosis: A Hybrid Memory- and Model-Based Approach».
- Prem Melville, Raymond J. Mooney, Ramadass Nagarajan «Content-Boosted Collaborative
Filtering for Improved Recommendations».
- Anne Yun-An Chen, Dennis McLeod «Collaborative Filtering for Information Recommendation
Systems».
- Luo Si, Rong Jin «Flexible Mixture Model for Collaborative Filtering».
- А.А Барсегян, М.С. Куприянов, И.И. Холод, М.Д. Тесс «Анализ данных и процессов»,
СПб.: БХВ-Петербург, 2009
 Скачать полную версию статьи Скачать полную версию статьи
|


