Кластеризация на основе нечетких отношений
Введение
Основные известные алгоритмы кластеризации (например, модификации алгоритмов K-Means, Expectation Maximization, реализованные, в том числе, в Microsoft Analysis Services 2005) налагают ограничения на геометрию получаемых кластеров, в частности, требуя возможности охвата каждого кластера отдельным выпуклым множеством. Такое ограничение налагается предположениями таких алгоритмов о существовании центров кластеров (K-Means) или функции плотности вероятности для каждого кластера с соответствующим значением математического ожидания и дисперсией (Expectation Maximization). В результате, эти алгоритмы не в состоянии адекватно разбить на кластеры невыпуклые множества, тем более вложенные структуры.
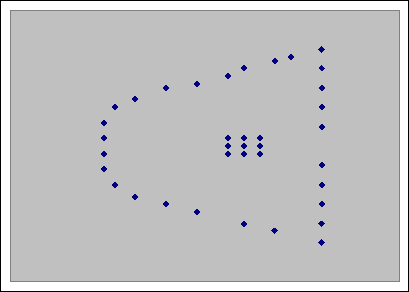
Такая необходимость возникает, например, для адекватной и информативной кластеризации демографических данных, описывающих зависимость возраста от дохода:
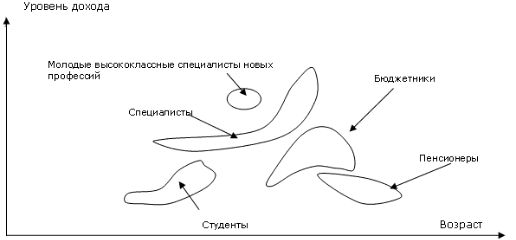
Эту проблему решает описываемый ниже алгоритм кластеризации на основе нечетких отношений, позволяющий группировать в кластеры элементы, между которыми есть последовательность "близких" друг к другу элементов, что также соответствует интуитивному представлению о группировке.
Алгоритм
Предлагается подход к кластеризации конечного набора элементов произвольного метрического пространства на основании разбиения множества на классы эквивалентности по нечеткому отношению.
На основании метрики определяется нечеткое отношение, обладающее свойствами четкой рефлексивности и нормальной -симметричности. Строится транзитивное замыкание отношения, позволяющее определить для каждого значения в диапазоне от 0 до 1 отношение эквивалентности на исходном множестве. По построению отношения два элемента входят в один класс эквивалентности тогда и только тогда, когда между ними есть последовательность попарно "близких" друг к другу элементов.
В случае если пространство кластеризуемых элементов является векторным пространством с топологией, индуцированной метрикой, то полученные при помощи описанного алгоритма кластеры могут иметь произвольную геометрическую форму, в том числе состоять из невыпуклых множеств. Это является значительным преимуществом подхода в сравнении с множеством известных алгоритмов кластеризации (например, модификациями алгоритма K-Means, Expectation Maximization и т.д.).
В числе преимуществ алгоритма можно назвать:
- Отсутствие необходимости в априорных предположениях относительно структуры данных (вид и параметры распределения вероятности по кластерам, центров плотности, числа кластеров).
- Понятная интерпретация результатов разбиения по кластерам: элементы входят в один кластер когда между ними есть последовательность близких друг к другу элементов.
- Отсутствие ограничений на геометрию кластеров.
- Время выполнения алгоритма мало зависит от числа компонент входных векторов.
Существенным недостатком алгоритма является большое время выполнения, характеризуемое порядком от числа элементов.
Математические основы
Данный раздел приведен в полной версии документа:
 Кластеризация на основе нечетких отношений. Алгоритм Fuzzy Relation Clastering
|
