Кластерный анализ
В статье рассматривается проблема определения внутренней структуры данных
при отсутствии какой-либо первоначальной информации о них. Эта проблема известна
как кластерный анализ, и ее следует отличать от дискриминантного анализа, в котором
уже осуществленное разбиение наблюдений по группам используется для категоризации
других наблюдений.
Методы кластерного анализа
Под кластерным анализом понимается задача разбиения исходных данных на
поддающиеся интерпретации группы, таким образом, чтобы элементы, входящие в
одну группу были максимально "схожи" (по какому-то заранее определенному
критерию), а элементы из разных групп были максимально "отличными" друг от
друга. При этом число групп может быть заранее неизвестно, также может не быть
никакой информации о внутренней структуре этих групп.
Методы кластеризации варьируются от достаточно эвристичных подходов до
формальных процедур основанных на методах математической статистики. Эти методы
в основном базируются на иерархической стратегии или на стратегии итеративного
перераспределения данных между различными кластерами для достижения оптимума
характерной для данного метода функции цели.
Иерархические методы
Иерархические методы формируют последовательность разбиений исходных данных
на кластеры. Каждый шаг этой последовательности разбиений делит данные на
различное число кластеров. Иерархические методы либо объединяют кластеры в
процессе реализации алгоритма либо разделяют их. Максимальное число кластеров в
этих алгоритмах ограничено. Наиболее известным иерархическим методом
кластеризации является метод ближайшего соседа: на первом шаге все элементы
представляют собой одноэлементные кластеры, а затем, в процессе реализации
алгоритма, в один кластер объединяются кластеры наиболее близко расположенные
друг от друга по какой-либо метрике. К иерархическим моделям также относятся
модели, объединяющие элементы исходных данных в кластеры, представляющие собой
классы эквивалентности, определяемые по пороговым значениям каких-либо метрик.
После получения последовательности таких разбиений, аналитик определяет
наиболее интересную и поддающуюся интерпретации модель. Таким образом, иерархические
методы кластеризации различаются алгоритмами разбиения или объединения данных
в кластеры, в то время как выбор результирующей модели с точки зрения числа
полученных кластеров остается за человеком.
Методы перераспределения
В методах перераспределения число кластеров задается изначально. Затем,
элементы исходных данных каким-либо образом (например, случайно) по возможности
равномерно приписываются к различным кластерам. Далее, итеративно каждый элемент
перераспределяется в другой кластер, оптимизируя определенную функцию цели, описывающую
качество полученной модели. Алгоритм завершается если нельзя больше перераспределить
элементы со значительным улучшением функции цели.
Наиболее известные методы перераспределения - это метод K-средних и метод
максимизации ожидания.
Метод K-средних (K-means)
Метод K-средних основан на минимизации суммы квадратов расстояний между
каждым элементом исходных данных и центром его кластера, т.е. функции
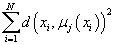 , где d - метрика, , где d - метрика,
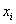 - i-ый элемент данных, а - i-ый элемент данных, а
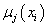 -центр кластера, которому на j-ой итерации приписан элемент -центр кластера, которому на j-ой итерации приписан элемент
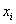 . .
Алгоритм
В простейшем случае, при выборе евклидовой метрики и числовых компонентах
исходных данных, алгоритм K-средних описывается следующим образом:
- j := 0. Случайно приписываем каждый элемент исходного множества одному из m кластеров.
- Определяем центр каждого кластера
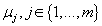 как элемент, компоненты которого вычисляются как среднее арифметическое компонент входящих
в этот кластер элементов. В центре кластера достигается минимум функции суммы квадратов
расстояний от элементов кластера до точки.
как элемент, компоненты которого вычисляются как среднее арифметическое компонент входящих
в этот кластер элементов. В центре кластера достигается минимум функции суммы квадратов
расстояний от элементов кластера до точки.
- Для каждого элемента вычисляем расстояние до центра каждого кластера. Элемент приписывается
к кластеру, расстояние до которого у него минимально.
- Если уменьшение суммы расстояния от каждого элемента до центра его кластера меньше порогового
значения, выходим.
- j++; goto 2
Сходимость
В процессе реализации алгоритма меняются значения центров кластеров (шаг 2) и
принадлежность элементов текущему кластеру (шаг 3). Каждое изменение на шаге 2
или 3 ведет к уменьшению функции цели. Таким образом, мы получаем монотонно
убывающую и ограниченную с низу, а следовательно, сходящуюся последовательность, т.е.
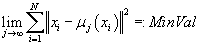 . Так как центры кластеров
ограничены компактным множеством (многомерный куб, образованный максимумами абсолютных
значений компонентов исходных данных), то последовательность центров кластеров
имеют сходящуюся к некому значению . Так как центры кластеров
ограничены компактным множеством (многомерный куб, образованный максимумами абсолютных
значений компонентов исходных данных), то последовательность центров кластеров
имеют сходящуюся к некому значению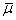 подпоследовательность, т.е.
подпоследовательность, т.е. 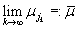 . Так как предел подпоследовательности равен пределу последовательности, а функция
цели как функция от центров кластеров непрерывна, то
. Так как предел подпоследовательности равен пределу последовательности, а функция
цели как функция от центров кластеров непрерывна, то
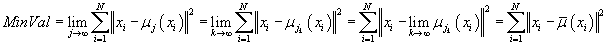 . .
Таким образом, из последовательностей центров кластеров, получаемых в процессе
реализации алгоритма, можно выделить подпоследовательность, сходящуюся к значению,
локально минимизирующему функцию цели.
Метод максимизации ожидания (EM - Expectation Maximization)
Метод максимизации ожидания основан на итеративном перераспределении исходных
данных между кластерами с целью максимизации функции правдоподобия данных как случайной выборки.
Модель
Пусть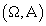 - пара из множества
элементарных событий и определенной на нем - пара из множества
элементарных событий и определенной на нем 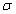 -алгебры. Пусть задано компактное s-мерное семейство параметров
-алгебры. Пусть задано компактное s-мерное семейство параметров 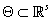 а на
а на 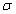 -алгебре задано семейство вероятностных мер -алгебре задано семейство вероятностных мер
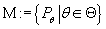 . Таким образом . Таким образом
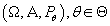 - семейство вероятностных пространств. - семейство вероятностных пространств.
Пусть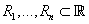 - множества значений
компонентов исходных данных, являющиеся подмножествами действительных чисел (каждое - множества значений
компонентов исходных данных, являющиеся подмножествами действительных чисел (каждое
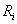 либо конечное, либо совпадающее с либо конечное, либо совпадающее с
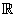 ). На каждом множестве ). На каждом множестве
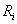 определена определена
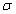 -алгебра -алгебра
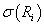 . В случае, если . В случае, если
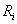 - конечное множество, то - конечное множество, то
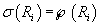 -множество всех подмножеств -множество всех подмножеств
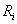 . Если . Если
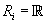 , то , то
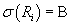 - борелевская алгебра. На множестве - борелевская алгебра. На множестве
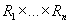 определена определена
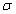 -алгебра как произведение соответствующих -алгебра как произведение соответствующих
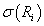 , т.е. , т.е.
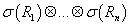 . .
Пусть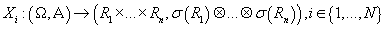 случайная n-мерная величина,
а i-ая строка исходных данных случайная n-мерная величина,
а i-ая строка исходных данных 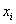 - ее реализация. Пусть
- ее реализация. Пусть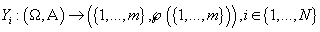 - случайная
величина, описывающая номер кластера, которому принадлежит - случайная
величина, описывающая номер кластера, которому принадлежит 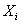 . Таким образом, случайная переменная
. Таким образом, случайная переменная
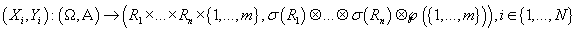
описывает реализацию i-ой строки исходных данных и соответствующий ей кластер.
Пусть на 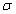 -алгебре -алгебре
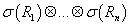 задана мера задана мера
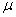 , а на , а на
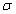 -алгебре -алгебре
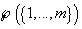 задана мера задана мера
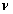 , ,
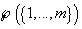 . Мы считаем, что для каждой меры из . Мы считаем, что для каждой меры из
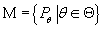 случайные величины случайные величины
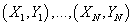 обладают следующими свойствами: обладают следующими свойствами:
- стохастически независимы, т.е.
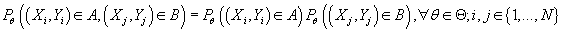 (1) (1)
- одинаково распределены, т.е.
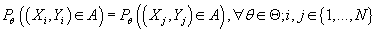 (2) (2)
- обладают совместной плотностью распределения
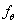 относительно меры
относительно меры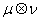 , т.е. , т.е.
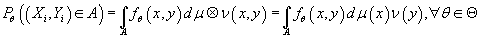 (3) (3)
Из пункта 3 следует, что плотность вероятности 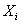 относительно
относительно 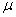 имеет вид: имеет вид:
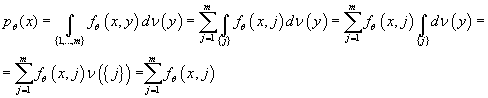
Плотность вероятности 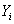 относительно относительно
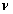 имеет вид: имеет вид:
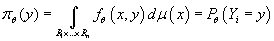 (4) (4)
Условная плотность вероятности 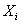 при условии
при условии 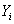 относительно относительно
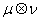 имеет вид: имеет вид:
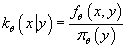 (5) (5)
Условная плотность вероятности 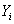 при условии
при условии 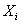 относительно относительно
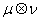 имеет вид: имеет вид:
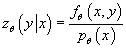 (6) (6)
Обозначим через 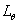 функцию
правдоподобия входных данных, т.е. значение плотности вероятности случайной величины функцию
правдоподобия входных данных, т.е. значение плотности вероятности случайной величины
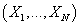 в точке реализации в точке реализации
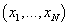 , т.е. , т.е.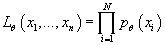 . .
Пусть 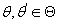 . Логарифм функции правдоподобия с параметром . Логарифм функции правдоподобия с параметром
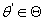 равен равен
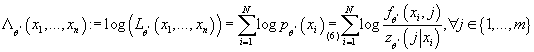 (7) (7)
Так как 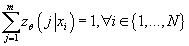 , с учетом (7) получаем: , с учетом (7) получаем:
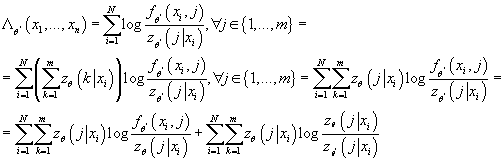 (8) (8)
Выражение 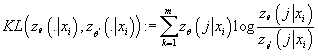 представляет собой
дивергенцию Кульбака-Лейблера от условных плотностей вероятности представляет собой
дивергенцию Кульбака-Лейблера от условных плотностей вероятности
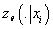 и
и 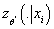 , которая является
неотрицательным значением. Следовательно, , которая является
неотрицательным значением. Следовательно,
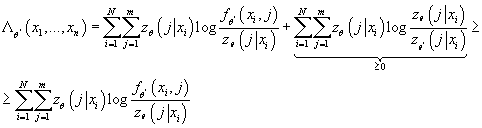 (9) (9)
Введем величины
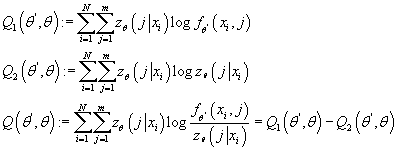 (10) (10)
Определим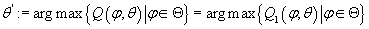 (11) (11)
Тогда из (8), (9) и (10) с учетом того, что
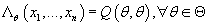 следует: следует:
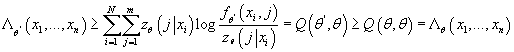 (12) (12)
Дополнительные условия
Пусть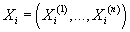 - компоненты
случайной величины - компоненты
случайной величины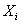 , причем , причем
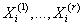 имеют непрерывное распределение, а имеют непрерывное распределение, а
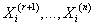 -дискретное. -дискретное.
Часто на модель накладываются дополнительные ограничения:
- Предполагается, что мера
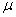 на
на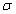 -алгебре -алгебре
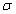 области значений
данных представляет собой произведение меры Лебега для непрерывных компонент
и дискретных мер для дискретных компонент. Т.е. области значений
данных представляет собой произведение меры Лебега для непрерывных компонент
и дискретных мер для дискретных компонент. Т.е.
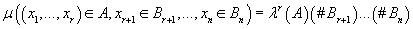
- Предполагается, что при известном значении кластера все непрерывные
компоненты случайной величины
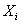 имеют совместное многомерное нормальное распределение, а каждая дискретная
компонента независима от всех остальных компонент и имеет мультиномиальное распределение.
имеют совместное многомерное нормальное распределение, а каждая дискретная
компонента независима от всех остальных компонент и имеет мультиномиальное распределение.
Тогда условная вероятность случайной величины 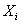 при известном номере кластера вычисляется следующим образом:
при известном номере кластера вычисляется следующим образом:
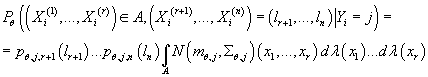
Где:
·
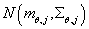 - функция
плотности многомерного нормального распределения, с вектором математического ожидания
и матрицей ковариаций параметризованными параметрами модели (итерацией алгоритма)
и значением кластера. - функция
плотности многомерного нормального распределения, с вектором математического ожидания
и матрицей ковариаций параметризованными параметрами модели (итерацией алгоритма)
и значением кластера.
·
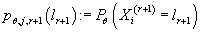 - вероятность
того, что r+1-ая (дискретная) компонента принимает значение - вероятность
того, что r+1-ая (дискретная) компонента принимает значение 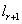 . Это значение также параметризовано параметрами модели (итерацией алгоритма) и значением кластера.
. Это значение также параметризовано параметрами модели (итерацией алгоритма) и значением кластера.
Таким образом, условная плотность вероятности 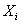 при известном значении
при известном значении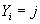 принимает вид: принимает вид:
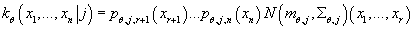 (13) (13)
Для определения функции совместной плотности распределения f нам также надо знать
значения вероятности принадлежности элемента данных к определенному кластеру, т.е.
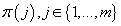 , которые мы добавляем в параметры модели. , которые мы добавляем в параметры модели.
Таким образом, на каждой итерации, параметрами модели являются величины:
·
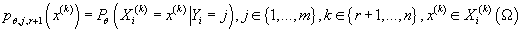 - вероятность
того, что в кластере j значение k-ой (дискретной) компоненты данных X принимает значение - вероятность
того, что в кластере j значение k-ой (дискретной) компоненты данных X принимает значение
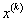 . Таких параметров . Таких параметров
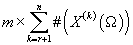 . .
·
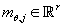 - вектор
математического ожидания непрерывной случайной величины - вектор
математического ожидания непрерывной случайной величины 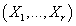 . .
·
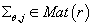 - симметричная
матрица ковариаций непрерывной случайной величины - симметричная
матрица ковариаций непрерывной случайной величины 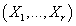 . .
·
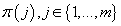 - вероятности
принадлежности элемента данных к кластеру j. - вероятности
принадлежности элемента данных к кластеру j.
Определим 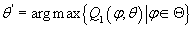 . Из (10) имеем: . Из (10) имеем:
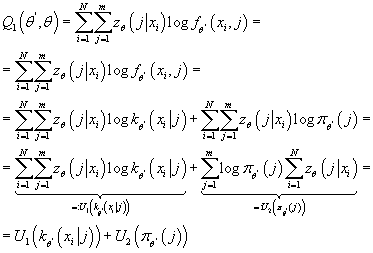 (14) (14)
Отсюда:
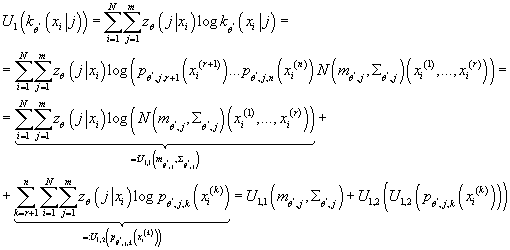 (15) (15)
Подставив выражение функции многомерной нормальной плотности распределения в
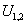 имеем: имеем:
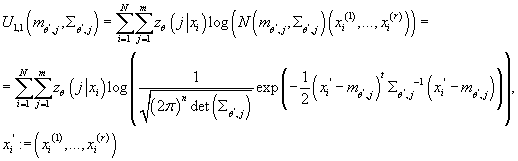
Отсюда:
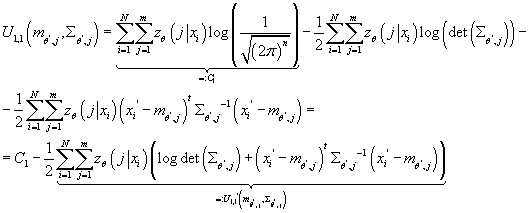 (16) (16)
Таким образом, для нахождения 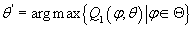 мы должны решить следующие задачи оптимизации:
мы должны решить следующие задачи оптимизации:
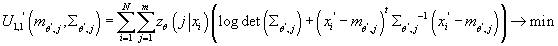 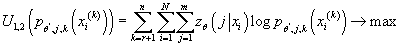 при ограничениях:
при ограничениях:

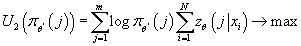 при ограничениях:
при ограничениях:
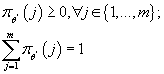
Решение задач 1-3 приведено ниже:
- Задача:
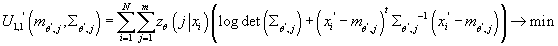
Задача максимизации по аргументу 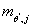 представляет собой задачу минимизации вогнутой дифференцируемой функции на
открытом множестве. Необходимым и достаточным условием является равенство
вектора частных производных по
представляет собой задачу минимизации вогнутой дифференцируемой функции на
открытом множестве. Необходимым и достаточным условием является равенство
вектора частных производных по 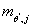 нулю. нулю.
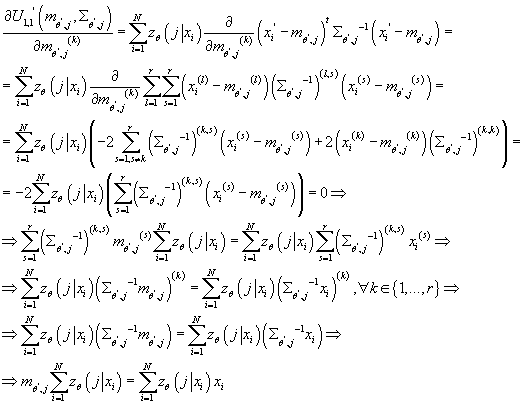
Таким образом, получаем:
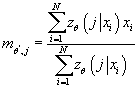 (17) (17)
Далее мы будем использовать следующие равенства:
·
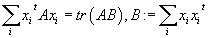
·
Если матрица A-симметричная и инвертируемая, то
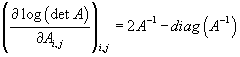
·
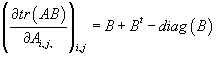
Получаем:
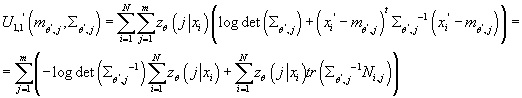
где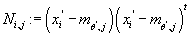
Берем производные от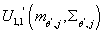 по по
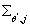 : :
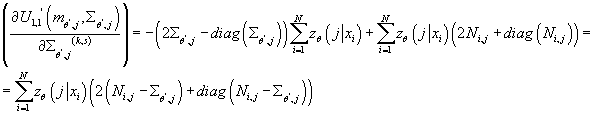
Определим:
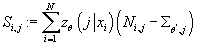 , тогда получим: , тогда получим:
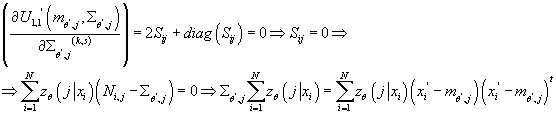
Получаем:
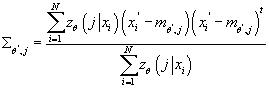 (18) (18)
- Задача:
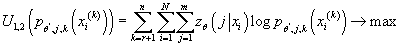 при ограничениях:
при ограничениях:

Эта задача является задачей максимизации выпуклой дифференцируемой функции
на множестве, заданном линейными ограничениями. Необходимым и достаточным
условием решения является значения аргументов, при которых градиент соответствующей
функции Лагранжа обращается в 0.
Функция Лагранжа для данной задачи выглядит следующим образом:
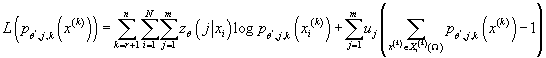
следовательно:
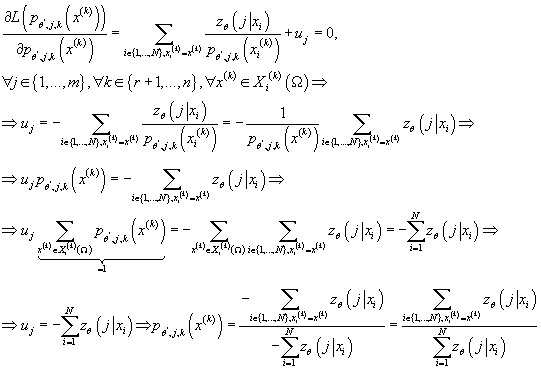
Таким образом:
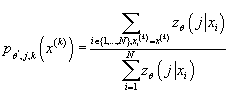 (19) (19)
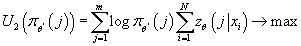 при ограничениях:
при ограничениях:
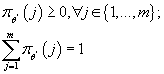
Эта задача является задачей максимизации выпуклой дифференцируемой функции
на на множестве, заданном линейными ограничениями. Необходимым и достаточным
условием решения является значения аргументов, при которых градиент соответствующей
функции Лагранжа обращается в 0.
Функция Лагранжа для данной задачи выглядит следующим образом:
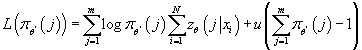
, следовательно
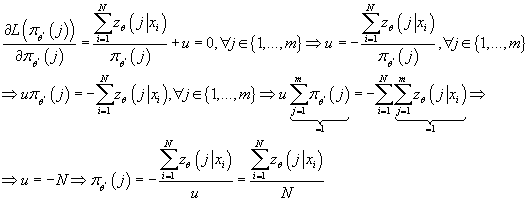
Следовательно
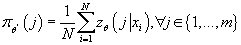 (20) (20)
Алгоритм
- Разбиваем каким-либо образом элементы входных данных по кластерам.
- Методом максимального правдоподобия вычисляем параметры условной плотности
вероятности
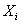 при известном значении кластера, т.е. определяем функцию
при известном значении кластера, т.е. определяем функцию
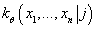 для каждого кластера j. для каждого кластера j.
Методом максимального правдоподобия вычисляем функцию
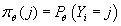 , т.е. вероятность
попадания произвольного элемента в каждый кластер. , т.е. вероятность
попадания произвольного элемента в каждый кластер.
Параметры функции 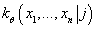 (вектор математического ожидания и матрица ковариаций непрерывных компонент и
значения вероятности дискретных компонент) и
(вектор математического ожидания и матрица ковариаций непрерывных компонент и
значения вероятности дискретных компонент) и
 (вероятности попадания элемента в кластер) образуют параметры модели
(вероятности попадания элемента в кластер) образуют параметры модели
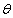 . .
- Вычисляем совместную плотность распределения
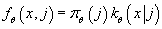 . .
- Вычисляем условную плотности вероятности попадания в кластер j при
известном значении
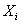 , т.е. определяем функцию
, т.е. определяем функцию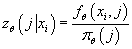 . .
- Вычисляем
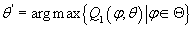 , где , где
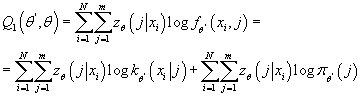
Получаем:
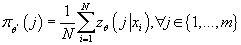
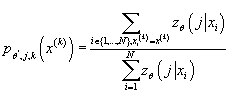
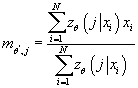
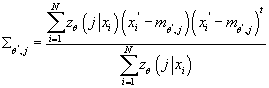
- Вычисляем условную плотность распределения входных данных
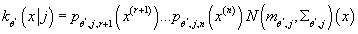
- Вычисляем совместную плотность распределения
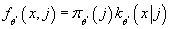
- Вычисляем функцию плотности распределения входных данных
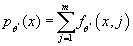
- Вычисляем логарифм функции правдоподобия
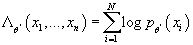
- Если
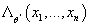 увеличился по сравнению с
увеличился по сравнению с 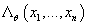 меньше, чем на пороговую величину, останавливаемся.
меньше, чем на пороговую величину, останавливаемся.
- Вычисляем условную плотности вероятности попадания в кластер j
при известном значении входного элемента, т.е. определяем функцию
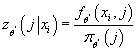
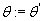 , goto 5. , goto 5.
Сходимость
Формула (12) гарантирует монотонный рост логарифма функции правдоподобия, которая
в свою очередь всегда является неположительной величиной, т.е. ограничена сверху.
Таким образом, логарифм функции правдоподобия сходится.
Параметры модели заключены в компактном множестве, следовательно, можно выделить
их сходящуюся подпоследовательность. Так как логарифм функции правдоподобия является
непрерывной функцией от параметров модели, то в значение предела подпоследовательности
параметров логарифм функции правдоподобия принимает свое предельное значение. Это
значение соответствует локальному максимуму функции правдоподобия исходных данных.
Методы определения числа кластеров
Общей проблемой в кластерном анализе является сложность определения "естественного"
числа кластеров в модели. Процесс определения числа кластеров часто связан с нахождением
баланса между решением задачи наиболее полного описания данных и ростом сложности
модели. Например, при использовании метода максимизации ожидания, мы не можем полагаться
на критерий правдоподобия данных для определения числа кластеров без учета сложности
модели, так как при возрастании числа кластеров в модели, правдоподобие данных будет
в этом случае также возрастать. Самая правдоподобная модель будет содержать число
кластеров равное числу элементов данных, и в этом случае каждый кластер будет
содержать только одну строку исходных данных. Однако, такая модель не будет иметь
никакой описательной и классификационной силы.
Метод разбиения исходного множества
Увеличение числа кластеров приводит к увеличению правдоподобия данных, на
которых производилось обучение, но при большой сложности модели происходит ее
"переобучение", т.е. подгонка параметров к частным особенностям обучающих данных,
а не к их структуре и имеющихся в них закономерностям. Т.е. на тестовых данных
(на данных, не участвовавших в обучении), сложная модель может показывать худшие
результаты, чем более простая, так как последняя учитывает только общие закономерности
в данных, а не особенности обучающей выборки.
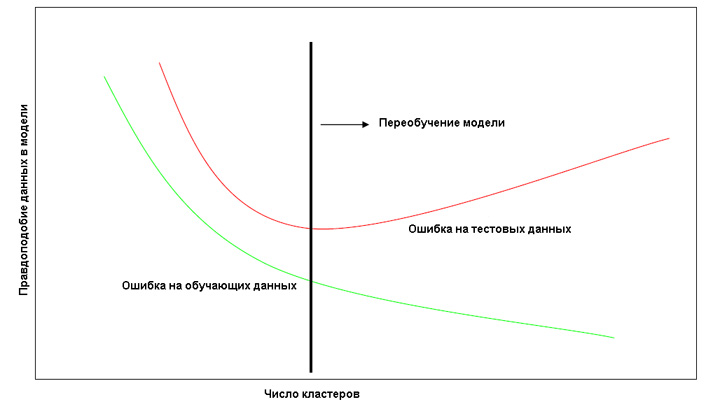
Рис. 1 График зависимости правдоподобия обучающей и тестовой выборки от числа кластеров в модели.
Этим соображением мотивирован подход, заключающийся в выборе модели, лучше
всего описывающей тестовые, а не обучающие данные.
Описание алгоритма:
- Исходные данные разделяются на две части: одна часть данных служит
для обучения модели, а другая - для тестирования. Разбиение производится
обычно в отношении 80/20 или 90/10.
- Мы начинаем с модели, описывающей данные при помощи одного кластера, т.е. s:=1.
- Если s больше порогового значения - останавливаемся.
- Для данного s мы производим обучение модели на обучающих данных,
т.е. получаем плотности распределения данных в каждом кластере модели, а
также функцию соответствия между произвольным элементом данных и номером кластера.
- При помощи полученной функции приписываем каждый элемент тестовых данных определенному кластеру.
- Вычисляем совместную функцию правдоподобия тестовых данных и
переменной класса. Если значение этой функции больше значения функции для
прошлой итерации - продолжаем итерации, т.е. s++, goto 3. В противном случае -
в качестве модели выбираем модель с числом кластеров s-1, останавливаемся.
Таким образом, алгоритм заключается в поиске первого локального максимума функции
правдоподобия тестовых данных от числа кластеров в модели.
Метод приведения к унимодальным распределениям
Алгоритмы кластеризации, оперирующие понятием центра кластера (такие как K-средние
или максимизация ожидания) обычно следуют допущению, что внутри каждого кластера данные
распределены по определенному унимодальному закону, например гауссовскому. Эти методы
предполагают, что каждый кластер описывается только одним центром (геометрический
центр точек в K-средних или математическое ожидание кластера в методе максимизации
ожидания), и этим центром является мода соответствующего распределения.
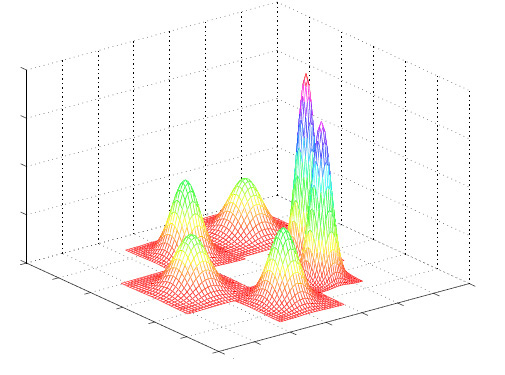
Рис. 2 Графики симметричных унимодальных плотностей распределения.
Это допущение интуитивно вполне объяснимо, так как попытка описания модели
при помощи групп с множеством центров в каждой группе привносит в модель
неоправданную степень сложности.
На основании этого соображения авторами Greg Hamerly, Charles Elkan был
предложен алгоритм G-means, который определяет число кластеров в модели на
основании последовательного выполнения статистического теста на то, что данные
внутри каждого кластера подчиняются определенному унимодальному закону распределения.
Если тест дает отрицательный результат, кластер разбивается на два новых кластера
с центрами, расположенными на оси главных компонент.
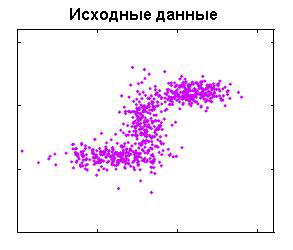 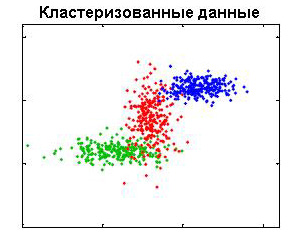
Рис. 3 Разбиение исходной выборки на кластеры с симметричными унимодальными распределениями.
Алгоритм G-means начинается с малого значения числа кластеров s. Каждая итерация
алгоритма разбивает центр одного кластера на два центра, если распределения данных
внутри этого кластера не подчиняется гауссовскому (или другому заранее выбранному
унимодальному симметричному) закону распределения. Между итерациями разбиения
кластеров выполняется алгоритм кластеризации методом k-средних или максимизации
ожидания для определения новых центров кластеров модели и распределения данных в них.
Для теста на соответствие эмпирической функции распределения данных внутри
кластера, являющегося кандидатом на разбиение, теоретической функции распределения
можно использовать большое количество хорошо известных статистик, например
Колмогорова-Смирнова. Авторы рекомендуют использование статистики Андерсона-Дарлинга,
как эмпирически наиболее точную и простую в вычислении.
При разбиении центра кластера на два новых, они помещаются на первой главной
компоненте распределения, соответствующего центру разбиваемого кластера.
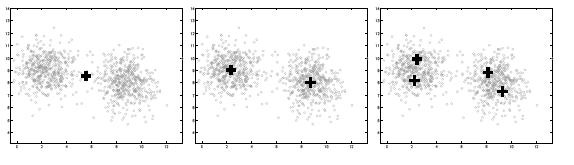
Рис. 4 Итеративное разбиение исходного множества на кластеры.
Байесовские методы
Пусть 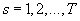 номера рассматриваемых
нами моделей-кандидатов, при этом s-ая модель описывает исходные данные при помощи s
кластеров. Каждая модель характеризуется априорной вероятностью номера рассматриваемых
нами моделей-кандидатов, при этом s-ая модель описывает исходные данные при помощи s
кластеров. Каждая модель характеризуется априорной вероятностью 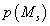 и параметрами распределения исходных данных
и параметрами распределения исходных данных 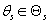 , которые подчиняются некому закону распределения с плотностью вероятности
, которые подчиняются некому закону распределения с плотностью вероятности
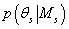 . Плотность вероятности
исходных данных в s-ой модели при известном значении параметра . Плотность вероятности
исходных данных в s-ой модели при известном значении параметра
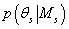 равна равна
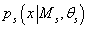 , таким образом,
выражение для плотности вероятности исходных данных x для s-ой модели будет иметь вид: , таким образом,
выражение для плотности вероятности исходных данных x для s-ой модели будет иметь вид:
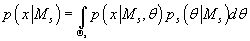 (21) (21)
Используя байесовский подход, получаем выражение для условной вероятности
s-ой модели при известных исходных данных:
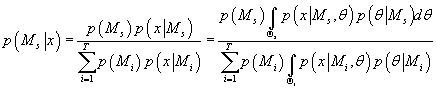 (22) (22)
Задача определения оптимальной модели будет заключаться в определении числа s,
для которого апостериорная вероятность соответствующей модели максимальна, т.е.
необходимо найти s, максимизирующее выражение (22).
Если мы предполагаем, что априори все модели равновероятны, т.е.
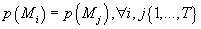 , то выражение (22) примет вид: , то выражение (22) примет вид:
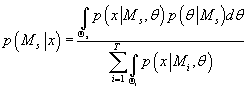 (23) (23)
Вследствие того, что знаменатель в (23) не зависит от номера текущей модели,
максимизация (23) эквивалента максимизации числителя, т.е.
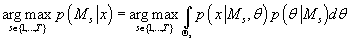 (24) (24)
Таким образом, задача определения наиболее вероятного с учетом исходных данных
числа кластеров в модели сводится к определению значения s, максимизирующего функцию
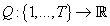
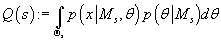 (25) (25)
Метод прямого интегрирования
Этот метод основан на явном задании вида априорных распределений 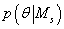 и численном вычислении интеграла в (25).
и численном вычислении интеграла в (25).
Для каждой модели мы предполагаем:
·
Исходные данные одинаково распределены и независимы.
·
Внутри каждого кластера все r непрерывных компонент исходных
данных имеют совместное многомерное нормальное распределение, а каждая из n-r
дискретных компонент условно (при известном значении кластера) независима от
всех остальных компонент и имеет мультиномиальное распределение.
Таким образом, для каждой модели 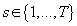 , для каждого кластера
, для каждого кластера 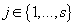 и для каждого элемента исходных данных
и для каждого элемента исходных данных 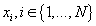 справедливо: справедливо:
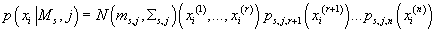 (26) (26)
Совместная плотность вероятности одного элемента исходных данных и соответствующего ему кластера равна:
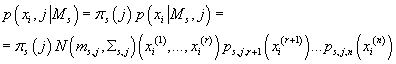 (27) (27)
Здесь 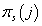 - априорная вероятность
j-ого кластера в s-ой модели. - априорная вероятность
j-ого кластера в s-ой модели.
Т.е., параметрами каждой модели, составляющие вектор 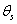 , являются величины:
, являются величины:
·
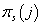 -
априорная вероятность j-ого кластера в s-ой модели. Ограничения: -
априорная вероятность j-ого кластера в s-ой модели. Ограничения:
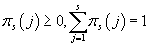 . В s-ой модели число таких параметров составляет s. . В s-ой модели число таких параметров составляет s.
·
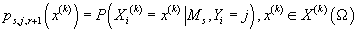 - вероятность того, что в модели s, в кластере j значение k-ой (дискретной) компоненты
данных X принимает значение
- вероятность того, что в модели s, в кластере j значение k-ой (дискретной) компоненты
данных X принимает значение 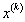 . Ограничения:
. Ограничения: 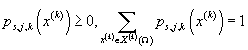 . В каждой модели таких число таких параметров составляет
. В каждой модели таких число таких параметров составляет 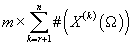 . .
·
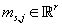 - вектор
математического ожидания непрерывной случайной величины - вектор
математического ожидания непрерывной случайной величины 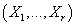 .
В каждой модели таких число таких параметров составляет r. .
В каждой модели таких число таких параметров составляет r.
·
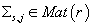 -
симметричная матрица ковариаций непрерывной случайной величины -
симметричная матрица ковариаций непрерывной случайной величины
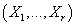 . В каждой модели таких
число таких параметров составляет . В каждой модели таких
число таких параметров составляет 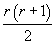 . .
Добавляя параметры модели 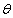 в аргументы
в аргументы 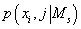 , мы можем переписать (27) в виде: , мы можем переписать (27) в виде:
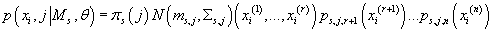 (28) (28)
Суммируя (28) по всем j, получаем плотность вероятности одного элемента данных
в s-ой модели как функцию от ее параметров:
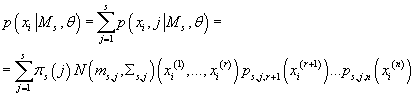 (29) (29)
С учетом независимости элементов исходных данных, получаем:
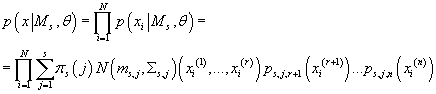 (30) (30)
Для того, чтобы вычислить функцию (25) нам необходимы предположения об априорном
распределении параметров модели. Обычной практикой в байесовском анализе является
выбор сопряженных плотностей, чтобы вид апостериорных функций плотностей совпадал
с априорными.
Для параметров дискретных распределений в модели (априорные распределения
кластеров, распределения дискретных компонент данных внутри каждого кластера)
мы выбираем равномерное распределение Дирихле, т.е.
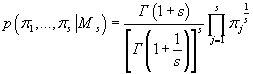 (31) (31)
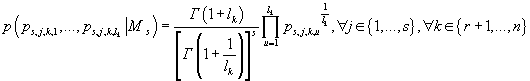 (32) (32)
Для параметров, соответствующих вектору математических ожиданий многомерного
нормального распределения непрерывных компонент внутри каждого кластера, мы можем
использовать либо нормальное, либо равномерное распределение. Для простоты выберем
равномерное, т.е.
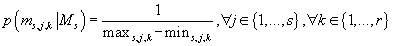 (33) (33)
Для априорного распределения параметров, соответствующих ковариационной матрице
непрерывных компонент, можно использовать обратное распределение Вишарта.
В простейшем случае, когда все непрерывные компоненты условно (при известном
значении кластера) независимы, можно использовать распределение Jeffrey для
параметров, соответствующих диагональным элементам ковариационной матрицы:
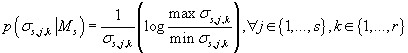 (34) (34)
Мы также предполагаем, что все компоненты вектора параметров
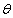 независимы,
т.е. с учетом (31)-(34) получаем: независимы,
т.е. с учетом (31)-(34) получаем:
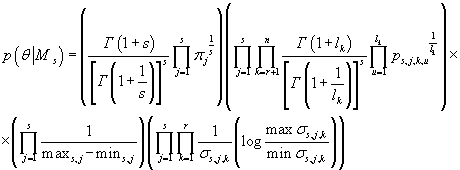 (35) (35)
Подставляя (30) и (35) в (25) получаем:
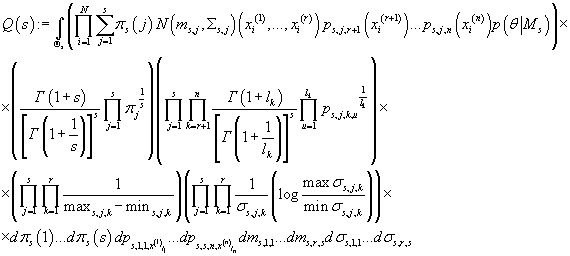 (36) (36)
Интегрирование в выражении (36) производится по множеству:
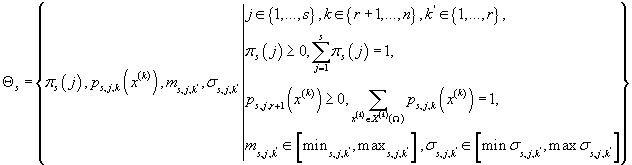 (37) (37)
Если число параметров в модели невелико (не больше 10), то интеграл (36) можно
вычислить каким-либо численным методом, например методом Монте-Карло.
В качестве решения задачи выбирается модель с числом кластеров s, которое является
первым максимум функции (36).
Информационный критерий Байеса
Непосредственное численное вычисление интеграла 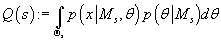 (25) является очень трудоемкой и ресурсоемкой задачей в большинстве реальных задач.
В этой связи закономерны поиски возможностей аппроксимации этого выражения. Основная
идея заключается в том, что при большом объеме выборки, выражение
(25) является очень трудоемкой и ресурсоемкой задачей в большинстве реальных задач.
В этой связи закономерны поиски возможностей аппроксимации этого выражения. Основная
идея заключается в том, что при большом объеме выборки, выражение
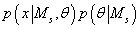 может быть аппроксимировано
функцией многомерного нормального распределения. может быть аппроксимировано
функцией многомерного нормального распределения.
Для каждого s определим функцию 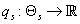
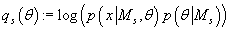 (38) (38)
Обозначим 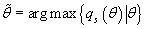 . Вследствие
монотонности логарифма, это значение также максимизирует функцию . Вследствие
монотонности логарифма, это значение также максимизирует функцию
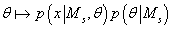 . Вследствие этого, значение
. Вследствие этого, значение 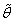 называется параметром максимальной апостериорной вероятности (maximum a posteriori probability - MAP)
исходных данных. Используя разложение Тейлора второго порядка для
называется параметром максимальной апостериорной вероятности (maximum a posteriori probability - MAP)
исходных данных. Используя разложение Тейлора второго порядка для
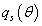 , получим: , получим:
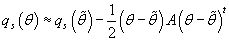 (39) (39)
где 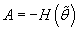 - негативное значение
матрицы вторых производных (дифференциал второго порядка) от - негативное значение
матрицы вторых производных (дифференциал второго порядка) от
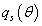 в точке в точке
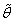 . .
Возводя e в степень левой и правой части выражения (39) получим:
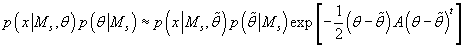 (40) (40)
Т.е. выражение (40) представляет собой нормальную (гауссовскую) аппроксимацию
подынтегрального выражения 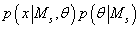 в (25).
в (25).
Интегрируя обе части выражения (40) по 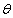 и беря логарифм, мы получаем аппроксимацию:
и беря логарифм, мы получаем аппроксимацию:
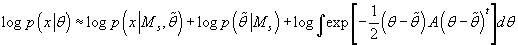 (41) (41)
Так как 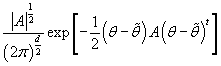 - плотность
d-мерного нормального распределения, то - плотность
d-мерного нормального распределения, то
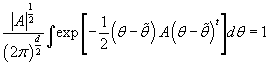 , а следовательно, , а следовательно,
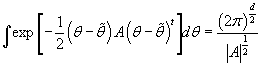 , т.е. с учетом (41) получаем: , т.е. с учетом (41) получаем:
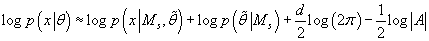 (42) (42)
Приведенная техника аппроксимации интеграла (25) называется методом Лапласа,
а выражение (42) - аппроксимацией Лапласа.
В работе Касса (Kass et al., 1988) было показано, что при определенных условиях,
относительная ошибка аппроксимации имеет порядок O(1/N), где N - размер выборки.
Таким образом, аппроксимация Лапласа может быть достаточно точной.
Можно получить эффективную с точки зрения вычисления (но менее точную) аппроксимацию
интеграла (25) оставив в выражении (42) только те члены, которые увеличиваются с ростом N:
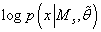 , которая растет линейно от N, , которая растет линейно от N,
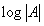 , которая растет как , которая растет как
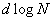 . Также, было показано,
что с ростом N максимальная апостериорная оценка . Также, было показано,
что с ростом N максимальная апостериорная оценка 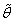 приближается к оценке максимального правдоподобия
приближается к оценке максимального правдоподобия 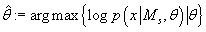 . Таким образом, мы получаем оценку:
. Таким образом, мы получаем оценку:
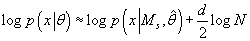 (43) (43)
Выражение (43) называется информационным критерием Байеса (Bayesian Information Criterion - BIC).
Оценка модели (в том числе определение числа кластеров при кластерном анализе)
на основании выражения (43) привлекательна по нескольким причинам:
- Оценка (43) не зависит от задания априорных распределений параметров
моделей, что существенно уменьшает субъективизм при их выборе.
- Оценка (43) интуитивно понятна: она состоит из слагаемого, описывающего
степень "подгонки" модели к данным, а также функцию "штрафа" за сложность
модели. Последнее обусловлено тем, что при усложнении модели, растет число
d - число ее параметров.
- Оценку (43) можно получить как оценку минимальной длины описания (
Minimum Description Length - MDL), т.е. на основании совершенно других рассуждений.
Таким образом, оценку (43) можно успешно использовать для оценки количества кластеров при кластерном анализе
Практические советы
Ниже собраны практические советы на основе опыта, полученного нами в процессе
реализации проектов по определению структуры данных.
·
Анализ данных является процессом. Определение паттернов в
данных является лишь началом цикла, куда затем входит этап содержательной
интерпретации, прогнозирования и тестирования.
·
Средства Data Mining общего назначения с параметрами по умолчанию
хороши только для предварительного анализа. После выявления предварительной структуры
данных средствами общего назначения следует подвергнуть полученную информацию
интерпретации экспертами в предметной области для формулирования содержательной
гипотезы о структуре данных. Затем, дальнейшие исследования следует проводить с
использованием механизмов, адаптированных для данной предметной области и учитывающих
специфику сформулированной гипотезы.
·
Следует с осторожностью относиться к неконтролируемой и
недокументированной обработке данных. Информация, содержащаяся в данных, попадающая
на вход аналитической системы, может быть подвергнута нормализации, калибровке,
исправлениям, сжатию, переформатированию и т.д., что может существенно снизить ее
ценность. Необходимо строго контролировать и учитывать возможные изменения входных данных.
·
Необходимо убедиться в релевантности, неискаженности и несмещенности
входных данных при формировании обучающих выборок.
·
Следует учитывать факт сложности получения информации от экспертов.
Эксперты склонны снабжать аналитиков только той информацией, которую они считают
важной. Поэтому аналитик должен сам становиться мини-экспертом в предметной области
для формулирования адекватных вопросов.
·
До выполнения сложных аналитических процедур необходимо провести
разведочный анализ существующих данных с максимальным использованием средств
графической визуализации. Это позволит составить самое общее представление о
данных, отбросить заведомо ложные гипотезы и дать направление последующему углубленному анализу.
·
Следует уделить большое внимание представлению результатов анализа.
Конечные пользователи увидят только то в вашей работе, что вы им представите.
Поэтому надо сделать форму представления результатов максимально ориентированную
на специфику конкретной задачи и предметной области потребителей информации.
 В формате PDF В формате PDF
|


