Модифицированный древовидный алгоритм Байеса для решения задач классификации
Описание задачи
Задача классификации – одна из наиболее распространенных
задач в анализе данных и распознавании образов. Для решения этой задачи требуется
создание классифицирующей функции, которая присваивает каждому набору входных
атрибутов значение метки одного из классов. Классификация входных значений
производится после прохождения этапа «обучения», в процессе которого на вход
обучающего алгоритма подаются входные данные с уже приписанными им значениями
классов.
На сегодняшний день разработано большое число подходов к
решению задач классификации, использующие такие алгоритмы как
·
деревья решений,
·
нейронные сети,
·
логистическая регрессия,
·
метод опорных векторов,
·
дискриминантный анализ,
·
ассоциативные правила.
Одним из эффективных алгоритмов классификации является так
называемый «наивный» (упрощенный) алгоритм Байеса. Точность классификации,
осуществляемой «наивным» алгоритмом Байеса, сравнима с точностью всех приведенных
выше алгоритмов. С точки зрения быстроты обучения, стабильности на различных
данных и простоты реализации, «наивный» алгоритм Байеса превосходит практически
все известные эффективные алгоритмы классификации.
Обучение алгоритма производится путем определения
относительных частот значений всех атрибутов входных данных при фиксированных
значениях атрибутов класса. Классификация осуществляется путем применения
правила Байеса для вычисления условной вероятности каждого класса для вектора
входных атрибутов. Входной вектор приписывается классу, условная вероятность
которого при данном значении входных атрибутов максимальна. «Наивность»
алгоритма заключается в предположении, что входные атрибуты условно (для
каждого значения класса) независимы друг от друга, т.е. 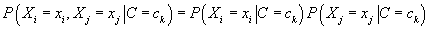 для всех
атрибутов Xi, Xj и значений класса C. Это предположение является очень сильным,
и, во многих случаях неправомерным, что делает факт эффективности классификации
при помощи «наивного» алгоритма Байес довольно неожиданным. для всех
атрибутов Xi, Xj и значений класса C. Это предположение является очень сильным,
и, во многих случаях неправомерным, что делает факт эффективности классификации
при помощи «наивного» алгоритма Байес довольно неожиданным.
В этой связи закономерен поиск таких модификаций в
алгоритме, которые ослабили бы предпосылку об условной независимости атрибутов.
Модификацией алгоритма, решающей эти проблемы, могут служить так называемые
байесовские сети. Байесовской сетью называется направленный граф без циклов,
позволяющий представлять совместное распределение случайных переменных. Каждый узел
графа представляет случайную переменную, а дуги – прямые зависимости между
ними. Более точно, сеть описывает следующие высказывание: каждая переменная зависит
только от непосредственных родителей. Таким образом, граф описывает ограничения
на зависимость переменных друг от друга, что уменьшает количество параметров
совместного распределения. Параметры совместного распределения кодируются в наборе
таблиц для каждой переменной в форме условных распределений при условии на
значения переменных-родителей. Структура графа и условные распределения узлов
при значениях их родителей однозначно описывают совместное распределение всех
переменных, что позволяет решать задачу классификации как определение значения
переменной класса, максимизирующее ее условную вероятность при заданных
значениях входных переменных.
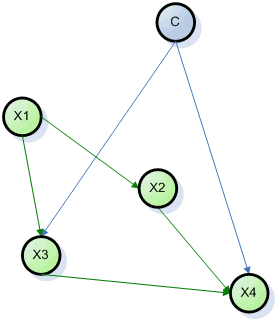
Байесовская сеть
Очевидно, что «наивный» алгоритм Байеса является частным
случаем байесовской сети, где каждая входная переменная зависит только от
переменной класса, которая является единственным корнем графа.
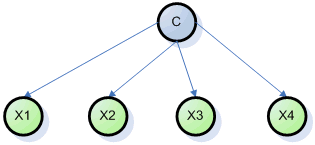
«Наивный» алгоритм Байеса
Обучение байесовских сетей стало одним из актуальных
направлением вычислительной математики и до сих пор является предметов активных
исследований. Однако, до сих пор определение структуры байесовской сети в общем
виде является сложной задачей как с теоретической, так и с вычислительной точки
зрения. Подход в общем виде обладает следующими недостатками:
·
Вычислительная сложность.
·
При попытке учесть большое количество зависимостей между
переменными, оценки условных вероятностей приобретают большую дисперсию, так
как их совместное появление в данных является маловероятным событием. Таким
образом, оценки параметров могут стать недостоверными, что в итоге может
приводить к ухудшению качества классификации даже по сравнению с «наивным»
алгоритмом Байеса.
·
Из-за большого количества параметров, модель получается слишком
ориентированной на обучающие данные. Это приводит к очень хорошим результатам
классификации на обучающих данных и неудовлетворительным результатам на
тестовых данных. Т.е. модель описывает не общие закономерности в структуре
данных, а скорее набор частных случаев в обучающей выборке.
Для решения этих проблем мы будем использовать ограничение
на структуру графа и рассматривать такое расширение «наивной» модели Байеса,
где каждый узел дополнительно может иметь не более одного родителя среди других
входных переменных.
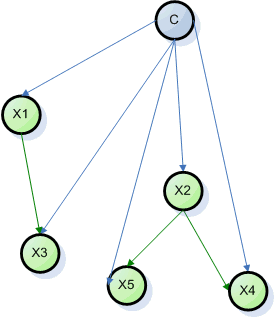
Модифицированный древовидный алгоритм Байеса
Описание алгоритма
Структура и параметры модели
Пусть 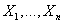 - дискретные
случайные переменные, область значений которых задана множествами - дискретные
случайные переменные, область значений которых задана множествами 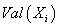 . .
Опишем зависимость переменных 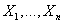 друг от друга с
помощью направленного ациклического графа G, узлами
которого являются переменные друг от друга с
помощью направленного ациклического графа G, узлами
которого являются переменные 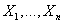 , а ребра задаются
функцией , а ребра задаются
функцией 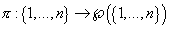 , ставящей в
соответствие каждому i-ому узлу графа множество родительских узлов , ставящей в
соответствие каждому i-ому узлу графа множество родительских узлов 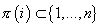 . Таким
образом, ребрами графа являются пары . Таким
образом, ребрами графа являются пары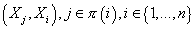 . .
Пусть задано семейство вероятностных мер 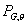 ,
параметризованное структурой графа G и параметрами распределения ,
параметризованное структурой графа G и параметрами распределения 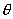 . Граф
G описывает независимость переменной . Граф
G описывает независимость переменной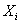 от переменных, не входящих в множество родительских узлов
от переменных, не входящих в множество родительских узлов 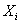 ,
т.е. ,
т.е.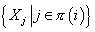 . Это означает . Это означает
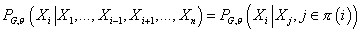 . (1) . (1)
Так как граф G является направленным ациклическим графом, то
его узлы можно разбить на уровни иерархии, т.е.
·
Первый уровень 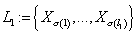 - узлы без
родительских узлов, т.е. - узлы без
родительских узлов, т.е. 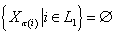
·
Второй уровень 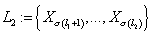 - узлы, у которых все
родительские узлы принадлежат первому уровню, т.е. - узлы, у которых все
родительские узлы принадлежат первому уровню, т.е. 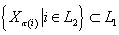
·
Третий уровень 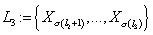 - узлы, у которых все
родительские узлы принадлежат первому или второму уровню, т.е. - узлы, у которых все
родительские узлы принадлежат первому или второму уровню, т.е. 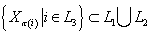
·
k-ый уровень 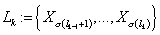 , ,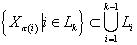
Таким образом, для графа G можно определить перестановку 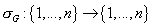 ,
которая упорядочивает узлы ,
которая упорядочивает узлы 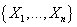 в порядке увеличения номеров
уровней графа. Внутри каждого уровня значение перестановки в порядке увеличения номеров
уровней графа. Внутри каждого уровня значение перестановки 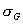 может
быть произвольным. может
быть произвольным.
Пусть 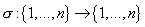 -произвольная
перестановка. Из определения условной вероятности следует выражение для
совместного распределения -произвольная
перестановка. Из определения условной вероятности следует выражение для
совместного распределения
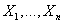 : :
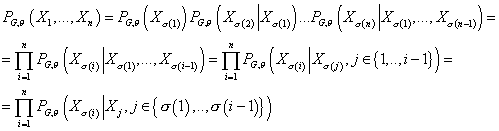 (2) (2)
Принимая во внимание выражение (1), т.е. зависимость каждой
переменной только от родительских узлов, выражение (2) приобретает вид:
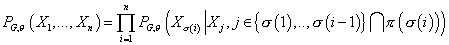 (3) (3)
Для перестановки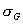 ,
упорядочивающей узлы ,
упорядочивающей узлы 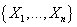 в порядке увеличения
номеров уровней графа, имеем: пусть k – номер уровня графа, куда входит элемент в порядке увеличения
номеров уровней графа, имеем: пусть k – номер уровня графа, куда входит элемент
 ,
т.е. ,
т.е. 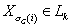 . Тогда элементы с большими
номерами чем . Тогда элементы с большими
номерами чем 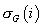 входят в уровни с
неменьшими номерами чем k, т.е. входят в уровни с
неменьшими номерами чем k, т.е. 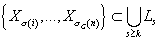 . Так как на каждом
уровне графа находятся элементы с родителями из уровней с меньшими номерами, то
родительские узлы элемента . Так как на каждом
уровне графа находятся элементы с родителями из уровней с меньшими номерами, то
родительские узлы элемента  принадлежит уровням
графа с меньшими номерами, чем номер уровня самого узла принадлежит уровням
графа с меньшими номерами, чем номер уровня самого узла , т.е. , т.е. 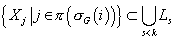 .
Из этого следует, что .
Из этого следует, что 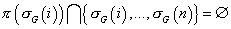 , а следовательно , а следовательно 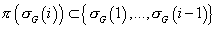 . .
Т.е. если мы в выражении (3) вместо произвольной
перестановки 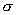 возьмем перестановку возьмем перестановку 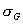 , то получим: , то получим:
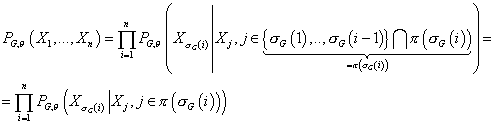 (4) (4)
Обозначим множество 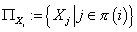 -
множество родителей переменной -
множество родителей переменной 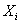 . Подставляя в (4) и
меняя порядок суммирования, получаем: . Подставляя в (4) и
меняя порядок суммирования, получаем: 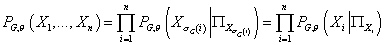 , т.е. , т.е.
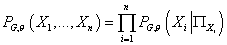 (5) (5)
Таким образом, совместное распределение вероятности
переменных 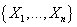 определяется заданием структуры
графа (т.е. набором родительских переменных определяется заданием структуры
графа (т.е. набором родительских переменных 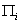 для
каждой переменной для
каждой переменной 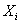 ) и параметрами
модели (т.е. величинами ) и параметрами
модели (т.е. величинами 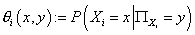 ). ).
Определение параметров модели
Обозначим 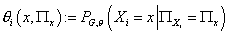 параметры модели в
выражении (5), где параметры модели в
выражении (5), где 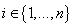 - индексы переменных, - индексы переменных, 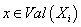 -
множество возможных значений i-той переменной, -
множество возможных значений i-той переменной, 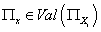 - множество возможных
значений родителей i-той переменной. - множество возможных
значений родителей i-той переменной.
Пусть вектора 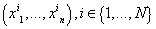 представляют собой N независимых реализаций случайной величины представляют собой N независимых реализаций случайной величины 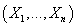 . Логарифм
функции правдоподобия параметров модели с учетом выборки D и структуры графа G принимает
вид: . Логарифм
функции правдоподобия параметров модели с учетом выборки D и структуры графа G принимает
вид:
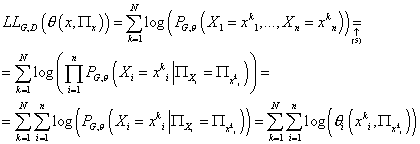 (6) (6)
На пространстве 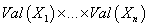 определим
вероятностную меру определим
вероятностную меру 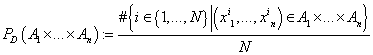 (7) (7)
как относительную частоту фактов вхождения векторов из
выборки D в данное множество.
С учетом определения этой меры можно заменить в выражении
(6) суммирование 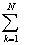 по всем значениям,
встречающимся в выборке D, на суммирование по всем
возможным значениям случайных переменных по всем значениям,
встречающимся в выборке D, на суммирование по всем
возможным значениям случайных переменных 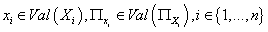 : :
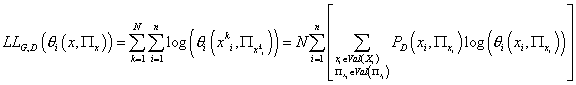 (8) (8)
Действительно, если вектор 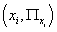 не
встречается в выборке D, то не
встречается в выборке D, то 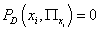 , т.е. он в
сумму не попадет. Если же он встречается p раз, то , т.е. он в
сумму не попадет. Если же он встречается p раз, то 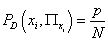 ,
т.е. он попадет в сумму p раз. ,
т.е. он попадет в сумму p раз.
Теперь мы можем использовать выражение (8) для нахождения
оценки максимального правдоподобия параметров модели 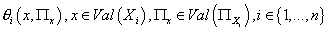 .
Для этого нам надо найти максимум функции .
Для этого нам надо найти максимум функции 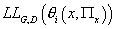 при ограничениях при ограничениях 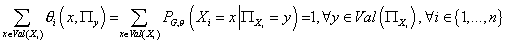 , (9) , (9)
т.е. сумма условных вероятностей всех различных реализаций
каждой переменной при любом фиксированном условии на значение родительских
переменных равна 1.
Целевая функция 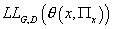 согласно выражению (8) непрерывно дифференцируема и вогнута
по согласно выражению (8) непрерывно дифференцируема и вогнута
по 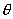 , функции
ограничений на , функции
ограничений на 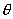 в выражении
(9) линейны. Следовательно, в выражении
(9) линейны. Следовательно, 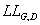 достигает
максимума на значении достигает
максимума на значении 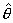 тогда и только
тогда, когда существует набор значений, соответствующий каждому ограничению,
т.е. числа тогда и только
тогда, когда существует набор значений, соответствующий каждому ограничению,
т.е. числа 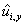 , где , где 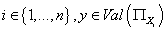 такие
что градиент функции Лагранжа, соответствующий задаче оптимизации, обращается в
ноль. Т.е. такие
что градиент функции Лагранжа, соответствующий задаче оптимизации, обращается в
ноль. Т.е.
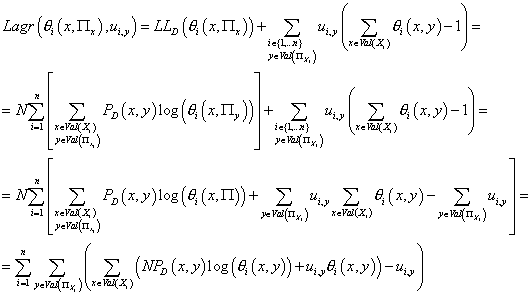 (10) (10)
Из (10) следует:
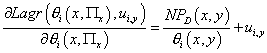 (11) (11)
Приравнивая (11) нулю, получаем значение параметров 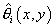 модели,
максимизирующие функцию (8) при ограничениях (9): модели,
максимизирующие функцию (8) при ограничениях (9):
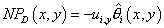 (12) (12)
Суммируя (12) по всем 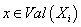 ,
получаем ,
получаем
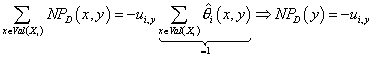 (13) (13)
Подставляя (13) в (12) получаем: 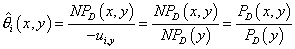 , ,
таким образом:
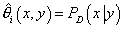 (14) (14)
Т.е. оценка параметров модели, максимизирующая функцию
правдоподобия по выборке определяется выражением (14) и равна относительным
условным частотам реализаций значений каждой переменной в выборке при
фиксированных значениях родительских переменных.
Принимая во внимание 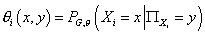 , получаем для оценки
из (14): , получаем для оценки
из (14): 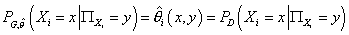 , (15) , (15)
т.е. оценка параметров модели, заданной графом G, методом
максимального правдоподобия по выборке D равна соответствующим выборочным
значениям.
Пусть вектора 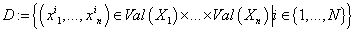 представляют собой N независимых реализаций случайной величины представляют собой N независимых реализаций случайной величины 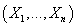 . .
Логарифм функции правдоподобия на выборке D
при фиксированной структуре модели, заданной графом G, как функция от
параметров модели принимает свой максимум согласно выражению (14) на значениях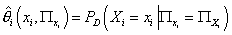 . .
Обозначим логарифм функции правдоподобия на выборке D с
оптимальными значениями параметров модели, вычисляемыми по формуле (14), как
функцию только от структуры модели, т.е. от графа G в следующем виде:
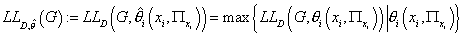 (16) (16)
Нашей следующей задачей будет нахождение максимума этой
функции на некотором подмножестве графов G, т.е. нахождение такой структуры
графа 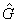 , что , что
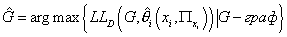
С учетом выражений (8), (14) и (16) получаем:
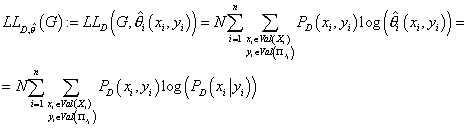 (17) (17)
Для величины взаимной информации между случайными величинами
X и Y, определяемой как 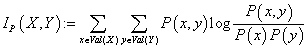 (18) (18)
и для величины энтропии случайной величины X, определяемой
как
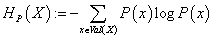 (19) (19)
получаем:
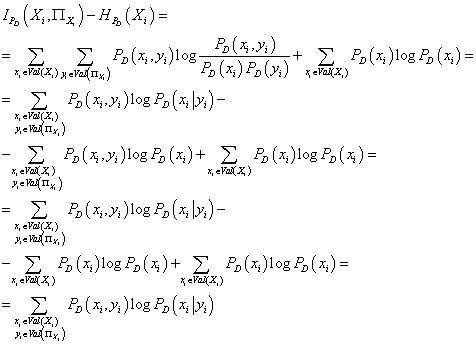 (20) (20)
Из (17) и (20) следует:
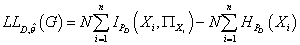 (21) (21)
Второе слагаемое в (21) не зависит от структуры модели, т.е.
от множеств 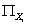 , поэтому задача
максимизации , поэтому задача
максимизации 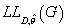 сводится к
максимизации первого слагаемого. Т.е. сводится к
максимизации первого слагаемого. Т.е.
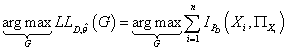 (22) (22)
Таким образом, оптимальная структура модели (с точки
зрения функции правдоподобия) соответствует модели с максимальной суммарной
взаимной информацией между узлами и их родителями.
Модель TAN - Tree Augmented Naive Bayes
Рассмотрим байесовские модели для решения задач
классификации. Т.е. среди рассматриваемых случайных переменных мы выделяем одну
переменную C (переменная класса), которую в дальнейшем мы будем обозначать
отдельно от остального набора переменных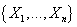 . .
За основу возьмем модель «наивного» (упрощенного) Байеса,
т.е. модель, где каждый узел зависит только от классифицирующей переменной. Т.е.
для «наивной» модели Байеса имеем: 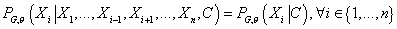 и и 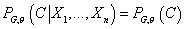 . Это условие
также можно сформулировать как . Это условие
также можно сформулировать как 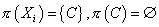 . .

Граф «наивной» модели Байеса.
Мы расширим «наивную» модель Байеса добавив взаимосвязи
между узлами модели. Однако, ограничимся рассмотрением только таких графов, где
у каждого узла не может быть более одного родителя за исключением узла C. Модель
с такими ограничениями называется в литературе TAN (Tree
Augmented Naive Bayes).
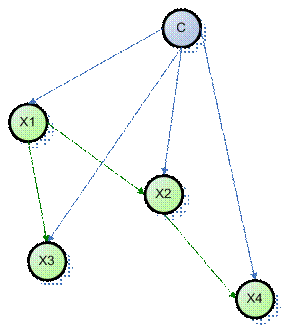
Граф модели TAN.
Модель TAN можно описать как
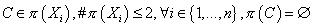 (23) (23)
Ниже мы определим оптимальную структуру для модели TAN.
Введем понятия условной по случайной величине Z взаимной
информации случайных величин X и Y:
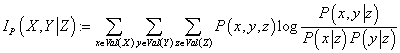 (24) (24)
Справедливо выражение:
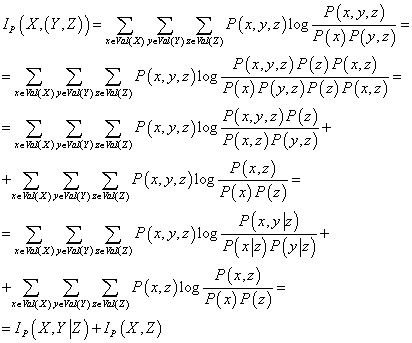 (25) (25)
Так как у классифицирующего узла C отсутствуют родители, то 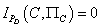 . .
Далее, по определению модели TAN
справедливо: 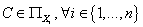 . Обозначим . Обозначим 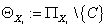 -
множество родителей узла -
множество родителей узла 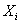 за исключением узла C.
Тогда за исключением узла C.
Тогда 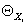 - либо пустое
множество, либо содержит только один узел из - либо пустое
множество, либо содержит только один узел из 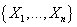 . .
Получаем:
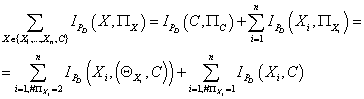 (26) (26)
Используя выражение (25) мы можем переписать (26):
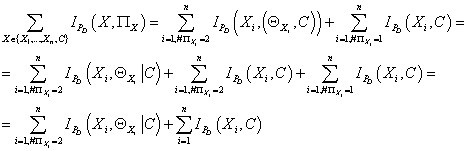 (27) (27)
Второе слагаемое в правой части (27) не зависит от структуры
модели, т.е. от множеств 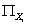 . Следовательно,
согласно (22), максимизация функции правдоподобия по структуре модели эквивалентна
максимизации второго слагаемого в правой части выражения (27), т.е. . Следовательно,
согласно (22), максимизация функции правдоподобия по структуре модели эквивалентна
максимизации второго слагаемого в правой части выражения (27), т.е.
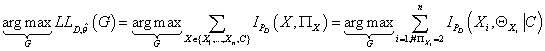 (28) (28)
Таким образом, оптимальная структура TAN-модели
(с точки зрения функции правдоподобия) соответствует модели с максимальной
суммарной условной по переменной класса взаимной информацией между узлами и их
родителями.
Мы теперь можем описать алгоритм определения оптимальной с
точки зрения максимизации функции правдоподобия TAN-структуры:
1. Для
каждой пары переменных 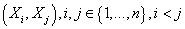 определяем величину
взаимной условной по C информации определяем величину
взаимной условной по C информации 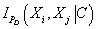 . .
2. Строим
ненаправленный полный граф с узлами из 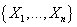 и дугами и дугами 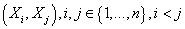 с
весами с
весами 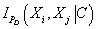 . .
3. Строим
дерево, соединяющее все вершины и имеющее максимальный суммарный вес, т.е.
максимальное покрывающее дерево. Такое дерево будет иметь максимальное значение
правой части в выражении (27) 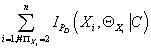 , а
следовательно, максимизировать функцию правдоподобия исходя из (28). , а
следовательно, максимизировать функцию правдоподобия исходя из (28).
4. Выбираем
узел, удовлетворяющий условию 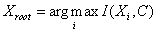 , и делаем его
вершиной графа. , и делаем его
вершиной графа.
5. Преобразуем
ненаправленный граф в направленной путем ориентации всех дуг от выбранного
корневого узла.
6. Добавляем
дуги из классифицирующего узла C ко
всем остальным узлам графа.
7. Вычисляем
оптимальные (с точки зрения максимизации функции правдоподобия) оценки
параметров распределения модели при уже определенной ее структуре по формуле
(15).
Получив оценку структуры и параметров модели, мы получаем
оценку совместного распределения вероятности всех переменных по формуле (5).
Модификация модели TAN
Очевидными недостатками приведенного алгоритма являются:
1. Случайный
выбор корневого узла, а, следовательно, направлений дуг.
2. Постулируемая
зависимость каждого узла от какого-либо другого узла не считая
классифицирующего. Таким образом, игнорируется возможность независимости
переменных друг от друга.
Для решения указанных проблем ниже мы опишем следующие модификации
алгоритма:
1. Определение
корневого узла как узла в наибольшей степени влияющего на исход
классифицирующей переменной C. В качестве критерия степени влияния выберем
взаимную информацию между каждым независимым узлом и классифицирующим узлом,
т.е. 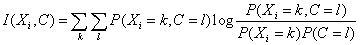
2. Введение
минимального порога на значение взаимной условной информации между узлами. Если
взаимная информация между узлами окажется меньше этого порога, мы будем считать
соответствующие узлы независимыми. В качестве такого порога выберем среднее
значение взаимной условной информации по всем узлам, т.е. 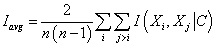
Алгоритм обучения модифицированной модели TAN:
1. Для
каждой пары переменных 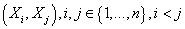 определяем величину
взаимной условной по C информации определяем величину
взаимной условной по C информации 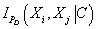 . .
2. Строим
ненаправленный полный граф с узлами из 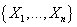 и дугами и дугами 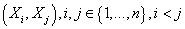 с
весами с
весами 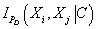 . .
3. Строим
дерево, соединяющее все вершины и имеющее максимальный суммарный вес, т.е.
максимальное покрывающее дерево. Такое дерево будет максимизировать функцию
правдоподобия на множестве всех TAN-структур.
4. Выбираем
узел, удовлетворяющий условию 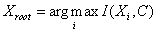 , и делаем его
вершиной графа. , и делаем его
вершиной графа.
5. Преобразуем
ненаправленный граф в направленной путем ориентации всех дуг от выбранного
корневого узла.
6. Добавляем
дуги из классифицирующего узла C ко
всем остальным узлам графа.
7. Удаляем
все дуги графа, у которых 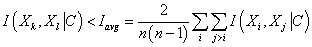
Таким образом, мы получаем структуру графа 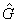
8. Вычисляем
оптимальные (с точки зрения максимизации функции правдоподобия) оценки
параметров распределения модели при уже определенной ее структуре по формуле
(15) 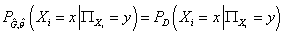 . .
Алгоритм классификации по обученной модели
Задача классификации по обученной модели заключается в
нахождении для каждого заданного вектора 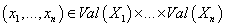 такого значения такого значения 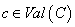 ,
что справедливо ,
что справедливо
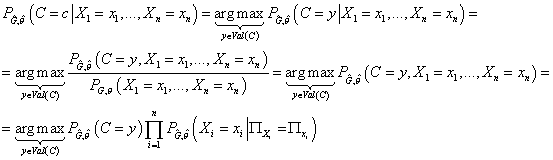
Для определения структуры графа в алгоритме определения
структуры модели мы должны найти максимальное покрывающее дерево. Приведем
алгоритм его определения.
Максимальное покрывающее дерево связанного графа –
дерево, соединяющее все вершины графа и имеющее максимальный суммарный вес.
Поиск минимального покрывающего дерева в графе (алгоритм
Прима)
1. Выбирается
произвольная вершина – корень покрывающего дерева.
2. Измеряется
расстояние от нее до всех других вершин. Это - расстояние до вершин от дерева.
3. До
тех пор пока в дерево не добавлены все вершины:
a. Найти
вершину, расстояние от дерева до которой максимально.
b. Добавить
ее к дереву.
c. Пересчитать
расстояния от вершин до дерева следующим образом: если расстояние от какой-либо
вершины дерева до какой-либо вершины графа больше текущего расстояния от дерева,
то старое расстояние от дерева этой вершины графа заменить новым.
 В формате PDF В формате PDF
|


